Lineární filtrace
Filtrací se označují takové operace, které vedou k oddělení užitečné a rušivé složky nebo také ke zvýraznění důležitých složek časových řad, jež jsou předmětem zpracování či analýzy. Termín filtrace sám o sobě upozorňuje na fakt, že cílem je určité složky propustit či zesílit a zároveň utlumit ty ostatní.
Ve výukové jednotce Systémy a jejich popis v časové a frekvenční oblasti bylo uvedeno, že LTI systém může požadovaným způsobem měnit frekvenční složení zpracovávaných časových řad. Takovýto systém, algoritmus nebo program, může být označen také jako filtr a jeden z mnoha způsobů jeho realizace pomocí operací sčítání, násobení a pomocí zpožďovacích členů z-1 je ukázán na obrázku 3.3. Je vidět, že koeficienty realizace diskrétního systému souvisejí přímo s koeficienty v jeho diferenční rovnici (3.7). Vyšší z čísel M a L udává vyšší stupeň z obou polynomů v rovnici (3.4) a označuje se jako řád filtru.
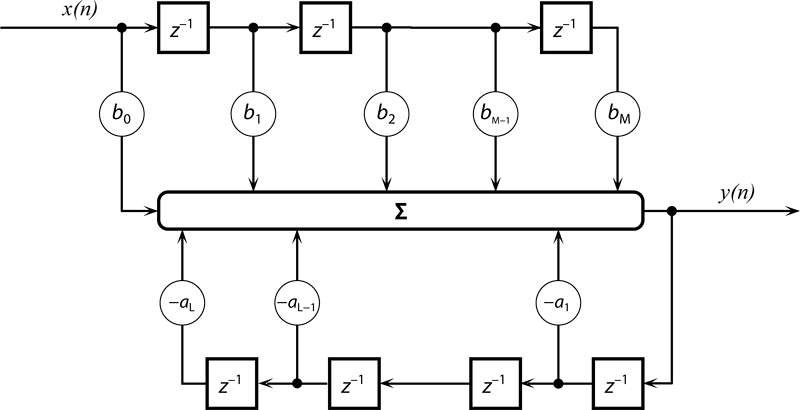
Obr. 3.3: Realizace filtru/programu/systému přímou formou. Realizační schéma i rovnici (3.7) je možno interpretovat tak, že LTI systém (nebo LTI filtr) uchovává v paměti starší vzorky časových řad na vstupu i na výstupu a jejich lineární kombinací počítá vzorky časové řady na výstupu.
Mohlo by se na první pohled zdát, že filtrování ve frekvenční doméně umožňuje libovolně tlumit nežádoucí harmonické složky časových řad. Pro tyto operace ve frekvenční doméně však existují určitá omezení, protože mohou jednak způsobovat podstatné oscilace v přenosové funkci filtru a dále mohou být příčinou nežádoucích přechodových dějů v časové doméně. Filtrování harmonických složek proto nelze ani v digitálním světě řešit ideálními filtry. Stanovení typu ideálního filtru je však výchozím bodem pro sestavení reálného filtru, jehož frekvenční charakteristika se obvykle blíží ideálnímu tvaru.
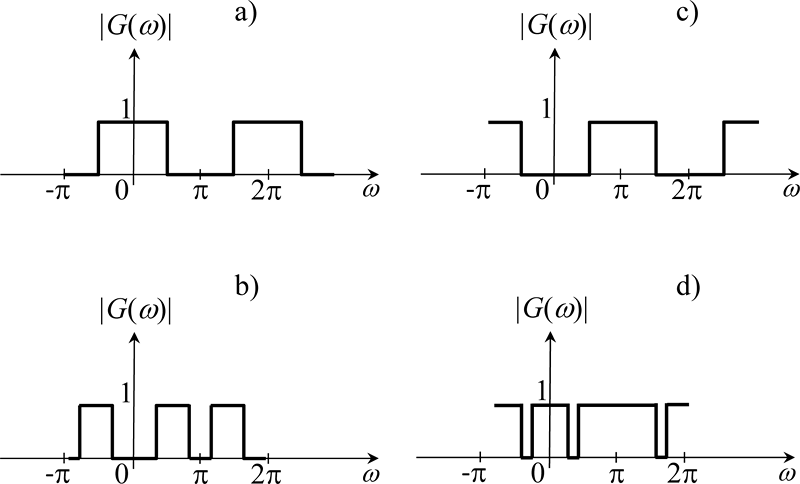
Na obrázku 2.3 a obrázku 3.4 jsou frekvenční charakteristiky ideálního filtru typu dolní propust, jehož účelem je zbavit časové řady rušivých složek o vysokých frekvencích. Filtrace horní propustí se využívá, pokud rušivé složky časových řad vykazují nižší frekvence než složky užitečné. Pokud užitečné složky časové řady leží v určitém frekvenčním pásmu, použije se pro jejich výběr filtr typu pásmová propust. Pro odstranění úzkopásmového rušení pak slouží filtr typu pásmová zádrž, viz obrázek 3.5.
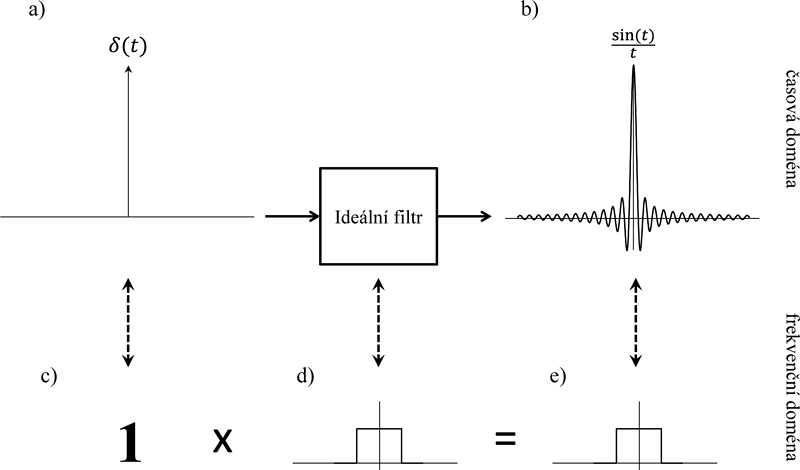
Obr. 3.4: Ideální filtr typu dolní propust by v případě své existence kompletně odstraňoval vysokofrekvenční složky a ponechával by beze změny nízkofrekvenční složky zpracovávaných časových řad. Takové chování odpovídá obdélníkové frekvenční charakteristice d), a to včetně záporných frekvencí. Výstup filtru ve frekvenční oblasti je dán součinem obrazu časové řady a frekvenční charakteristiky filtru e). Odezva takového systému v časové oblasti – impulsní charakteristika b) – na jednotkový impuls a) brání v existenci takového systému, neboť odezva je nenulová pro časy t<0. V analogovém světě nelze ideální filtr realizovat, poněvadž jde o nekauzální systém. V digitálním světě nelze ideální filtr realizovat, poněvadž impulsní charakteristika pro svůj rozsah od -∞ do +∞ vyžaduje nekonečnou paměť a frekvenční charakteristika obsahuje nekonečně strmé náběžné a sestupné hrany. Na obrázku jsou frekvenční charakteristiky a spektra znázorněna jen ilustrativně, bez fázových částí.
Obr. 3.5: Modulové frekvenční charakteristiky a) ideální dolní propusti,
b) ideální pásmové propusti, c) ideální horní propusti a d) ideální pásmové zádrže.