Úlohy k procvičení

ÚLOHA 1: Simulujte měření 1000 časových řad představujících směsi užitečné a rušivé složky. Naměřené hodnoty následně použijte při kumulačním zpracování s rovnoměrnými i exponenciálními vahami. Pro generátor repetic měřené časové řady vytvořte funkci, jejímž výstupem bude směs užitečné složky a náhodné rušivé složky a dále i obě složky separátně. Užitečná složka má sinusový průběh s lineárně narůstající frekvencí – tzv. chirp signál. Rušivou složkou bude šum s uniformním rozdělením pravděpodobnosti a nulovou střední hodnotou. Poměr šumu ve směsi definujte pomocí SNR v decibelech. Simulovaná data využijte pro ověření teoretických poznatků z této výukové jednotky v následujících dílčích úkolech:

1. Vykreslete výslednou repetici po kumulaci s rovnoměrnými vahami a porovnejte s průběhy repetic před kumulací.
2. Vykreslete výslednou repetici po kumulaci s exponenciálními vahami nastavenými tak, aby výsledné zlepšení poměru signál šum bylo stejné jako v případě rovnoměrné kumulace.
3. Vykreslete dynamické vlastnosti obou kumulačních metod a popište, jak se obě metody liší. U rovnoměrné kumulace zvažujte obě varianty – s pevným a s plovoucím oknem.
4. Pro případ rovnoměrné kumulace odhadněte zbytkovou rušivou složku a zjistěte, zda vypočtené průměrné zlepšení poměru signálu k šumu odpovídá zlepšení vypočtenému z experimentálních dat.

Řešení

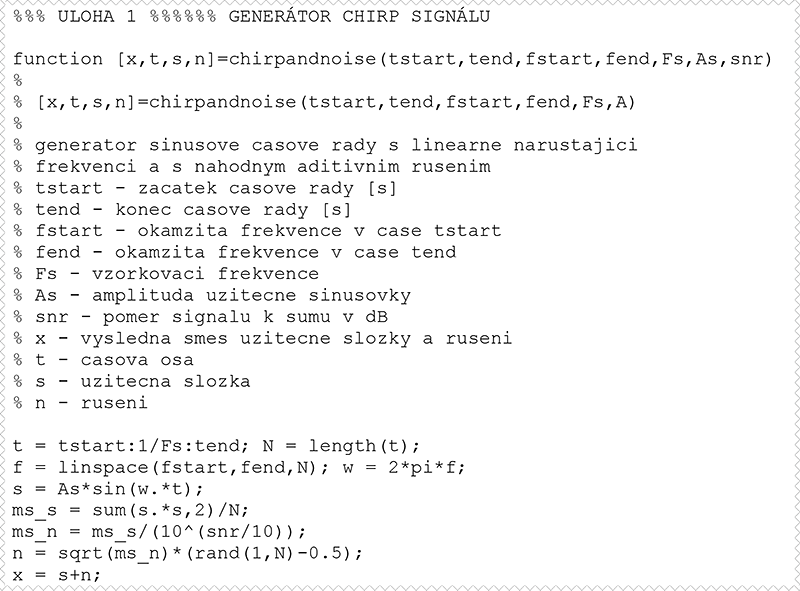
Kód funkce pro generování časových řad s lineárně rostoucí frekvencí je na obr. 9. Amplituda šumu generovaného funkcí rand() je odvozena z rovnice (5.3) pro SNR:

Obr. 5.9: Úloha 1 – funkce pro generování časových řad s lineárně rostoucí frekvencí a aditivním šumem s nulovou střední hodnotou a uniformním rozdělením pravděpodobnosti.

 

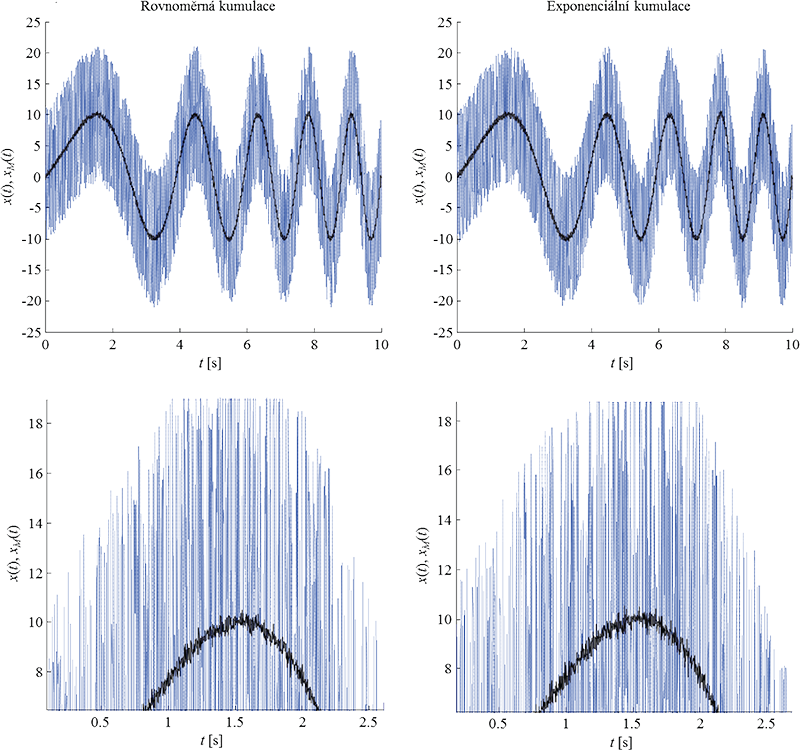
Obr. 5.10: Úloha 1 – slabou tečkovanou čarou jsou vykresleny vybrané jednotlivé repetice před kumulací a silnou plnou černou čarou je vykreslena zvýrazněná užitečná složka: vlevo pomocí kumulace s rovnoměrnými vahami, M=1000 a vpravo pomocí kumulace s exponenciálními vahami, M=1000, a=(M-1)/(M+1)). Nahoře jsou průběhy celé repetice, dole jsou pak vybrané detaily pro ilustraci, že výsledky obou metod se okometricky neliší.

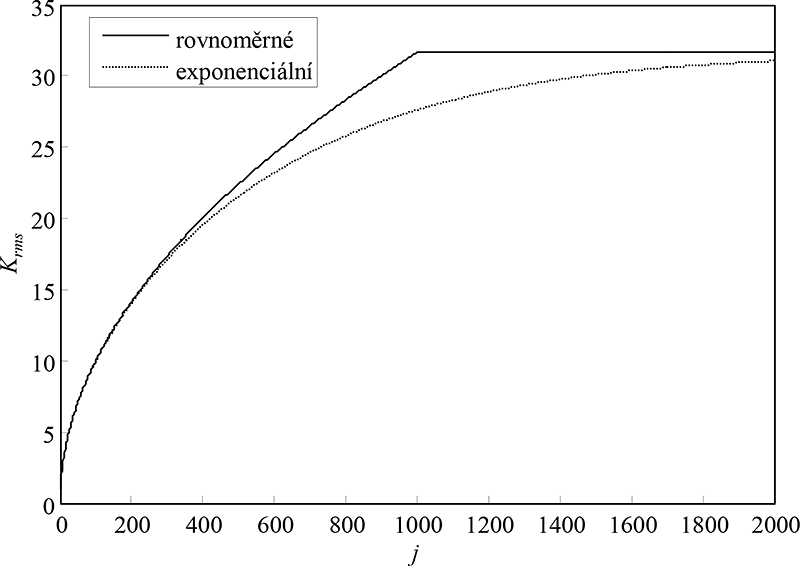
Kód programu v Matlabu, realizující řešení všech dílčích úkolů, je na obr. 5.13. Simulovaná data představují opakovaná měření stejného jevu, a tak není třeba se zabývat stanovováním referenčních časových souřadnic – všechny repetice vygenerované funkcí chirpandnoise() jsou v časové koherenci.  Obr. 5.10 ukazuje jednak vybrané repetice, u nichž lze pozorovat pro zvolené SNR = -10 dB překrytí užitečné složky šumem a dále ukazuje zvýrazněnou užitečnou složku pomocí rovnoměrné i exponenciální kumulace. Dynamické vlastnosti jsou na obr. 5.11 vykresleny pro 2M repetic, a to pro případ, že by se u kumulace s rovnoměrnými vahami pokračovalo od 1001. repetice s klouzavým oknem. U rovnoměrné kumulace lze pozorovat rychlejší dosažení nejvyššího možného průměrného zlepšení poměru signálu k šumu, než je tomu u exponenciální kumulace.

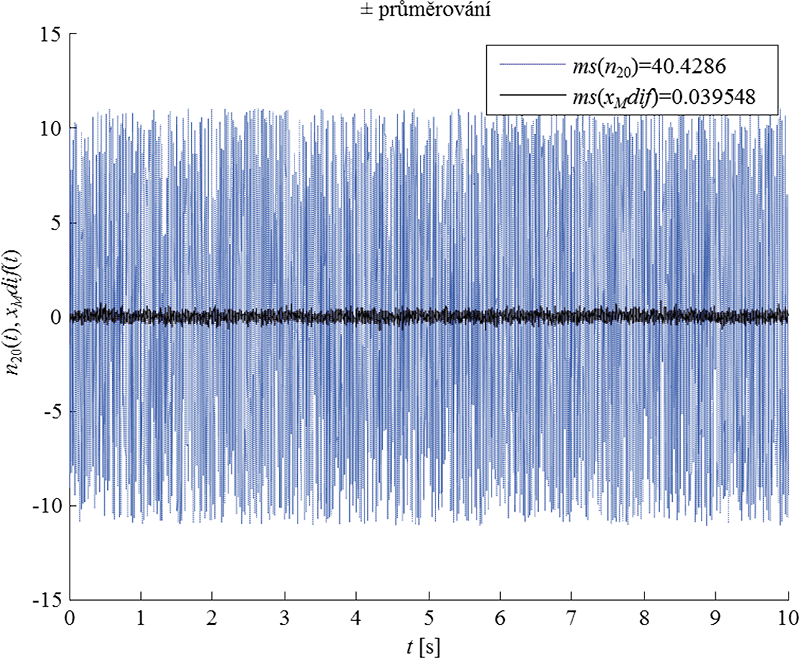
Výsledek ± průměrování pro odhad zbytkové rušivé složky je na obr. 5.12, a to společně s výsledkem výpočtu průměrných výkonů rušivé složky v jedné vybrané repetici před kumulací ms(n₂₀(t)) a reziduální rušivé složky po kumulaci. Z výsledků je patrné, že vlivem kumulace došlo k 1000-násobnému utlumení průměrného výkonu rušivé složky, což při zachování výkonu užitečné složky repetiční časové řady vede na 1000-násobné zlepšení výkonového poměru signálu k šumu a cca 32-násobné zlepšení amplitudového poměru signálu k šumu, což je v souladu s výsledkem na obr. 5.11 a s teoretickými poznatky této výukové jednotky.

Obr. 5.11: Úloha 1 – porovnání dynamických vlastností kumulace s rovnoměrnými a exponenciálními vahami. V případě rovnoměrné kumulace je od 1001. repetice použit algoritmus s klouzajícím oknem.

Obr. 5.12: Úloha 1 – ukázka jedné realizace rušivé složky (slabou tečkovanou čarou)
a výstup z ± průměrování (silnou plnou čarou), jehož výsledkem je zbytková rušivá složka po rovnoměrné kumulaci. Dále jsou zde vypočítané průměrné výkony obou náhodných časových řad, ze kterých je vidět, že vlivem kumulace 1000 směsí užitečné a náhodné rušivé složky došlo ke snížení průměrného výkonu rušivé složky přibližně 1000-krát.

Obr. 5.13: Úloha 1 – řešení v Matlabu.