Zobrazení, funkce, operace

Pojem zobrazení vychází z pojmu relace. Zatímco relace definovala nějaký obecný vztah mezi libovolnými dvojicemi prvků daných množin, zobrazení je tu od toho, aby každému prvku jedné množiny přiřadilo (obecně jiný) prvek téže, nebo jiné množiny. Z toho tedy vyplývá ona důležitá omezující podmínka, že každý prvek množiny  může být v relaci maximálně s jediným prvkem množiny .

Zobrazení: Nechť ,  jsou množiny. Zobrazením množiny  do množiny  nazýváme každou relaci , pro kterou platí: každému prvku  je přiřazen nejvýše jeden takový prvek , že uspořádaná dvojice . Skutečnost, že je zobrazením množiny  do množiny  značíme

Funkce: Jsou-li navíc  a  číselné množiny, hovoříme namísto zobrazení o funkci. Namísto budeme nyní psát . Umožňuje nám to právě podmínka jednoznačnosti prvku  ve vztahu k prvku . O prvku  budeme hovořit jako o vzoru prvku , o prvku pak budeme hovořit jako o obrazu prvku .

Definiční obor: Podle definice zobrazení má být každému prvku množiny  přiřazen nejvýše jeden prvek množiny . Znamená to tedy, že v množině  mohou existovat jak prvky, kterým není přiřazen žádný prvek z množiny , tak prvky, kterým je přiřazen jeden prvek z množiny . Platí tedy, že pokud, pak množinu definovanou jako nazveme definičním oborem zobrazení (značíme ). Definiční obor zobrazení je tedy množina všech prvků, pro něž má zobrazení smysl (je definováno).

Obor hodnot: Nechť ,  jsou množiny a   je zobrazení . Pak množinu definovanou jako nazveme obor hodnot zobrazení (značíme ). Obor hodnot je tedy zjednodušeně řečeno "množina obrazů", čili množina všech prvků množiny , které mají svůj vzor v množině .

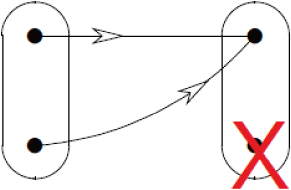Surjektivní zobrazení: Nechť ,  jsou množiny a je zobrazení . Jestliže , to znamená , říkáme, že zobrazení je zobrazení na množinu . Zobrazení na množinu se též nazývá surjektivní zobrazení, neboli surjekce.

Příklad: Jsou zobrazení f: N→ N definované vztahem f(x) = x + 1 a zobrazení g: N→ N₀ definované vztahem g(x) = x-1 surjektivní?

Řešení

Zobrazení f není surjektivní, neboť existuje přirozené číslo 1, které nemá svůj vzor (číslo 0 které by mohlo být jeho vzorem nepatří mezi přirozená čísla). Zobrazení g je surjektivní, neboť každé přirozené číslo a nula má v definičním oboru (množině přirozených čísel) svůj vzor.

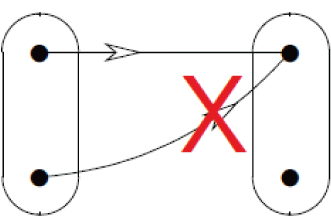Prosté zobrazení, injekce: V definici zobrazení jsme požadovali, aby každému prvku z definičního oboru byl přiřazený pouze jediný prvek z oboru hodnot. To však ještě nevylučuje případ, kdy je jeden prvek z oboru hodnot obrazem více prvků definičního oboru. To nás vede k definici prostého zobrazení, které právě tuto násobnost přiiřazení vylučuje. Nechť ,  jsou množiny a je zobrazení . Jestliže , pak říkáme, že zobrazení je prosté. Prosté zobrazení též nazýváme injektivní zobrazení, neboli injekce.

Příklad: Určete, zda je zobrazení f: R → R: f(x) = x² prosté (injektivní).

Řešení

Zobrazení f prosté není, neboť f(x) = f(-x) pro všechna reálná čísla.

 

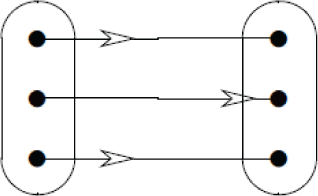Bijekce: Zobrazení, které je zároveň injektivní a surjektivní se nazývá bijektivní zobrazení, neboli bijekce. Existuje-li mezi dvěma množinami bijektivní zobrazení, pak je zřejmé, že tyto dvě množiny musí mít stejný počet prvků. Je-li totiž každému prvku definičního oboru přiřazen právě jeden prvek oboru hodnot (protože je to zobrazení), každý prvek oboru hodnot má svůj vzor v definičním oboru (protože je to surjekce) a tento vzor je navíc určen jednoznačně (protože je to injekce), jedná se o párování 1:1, které je evidentně možné realizovat jedině mezi stejně početnými množinami.

Příklad bijektivního zobrazení: f:{a,b,c,d} → {1,2,3,4}: f(a)=1, f(b)=2, f(c)=3, f(d)=4

Inverzní zobrazení: Nehchť ,  jsou množiny a je binární zobrazení. Inverzní zobrazení k zobrazení pak můžeme definovat takto: .

Příklad: Je dáno zobrazení f:{a,b,c,d} → {1,2,3,4}: f(a)=1, f(b)=2, f(c)=3, f(d)=4. Určete k němu inverzní zobrazení.

Řešení

g: {1,2,3,4} → {a,b,c,d}: g(1)=a, g(2)=b, g(3)=c, g(4)=d je inverzním zobrazením k zobrazení f.

U zobrazení daných výčtem je problém určení inverzního zobrazení řešitelný velmi snadno. Je-li zobrazení dáno funkčním předpisem, je třeba zaměnit význam proměnných a vyjádřit novou neznámou. Ukažme si tento postup na následujícím příkladu.

Příklad: Je dáno zobrazení f: R → R: . Určete k němu inverzní zobrazení.

Řešení

Pro jednoduchost provedeme substituci y = f(x) a dostáváme . V tomto vzorci zaměníme x a y (tím jsme definovali invezní zobrazení): . Zbývá už jen vyjádřit y, abychom získali přepis inverzního zobrazení: 2x = y-3 ⇒ y = 2x + 3. Inverzní zobrazení tedy je f^-1: R → R: f^-1(x) = 2x + 3.

Složené zobrazení: Jsou li dány množiny , ,  a zobrazení a , pak definujeme složené zobrazení , značíme , vztahem: . Složené zobrazení tedy vzniká postupnou aplikací obou skládaných zobrazení.

Příklad: Jsou dány zobrazení f: R → R: f(x) = x³ a g: R → R: f(x) = 2(x+3). Určete, jak vypadají složená zobrazení g º f a f º g.

Řešení

Složené zobrazení g º f: R → R: g º f(x) = g(f(x)) = 2(f(x)+3) = 2(x³+3)

Složené zobrazení f º g: R → R: f º g(x) = f º 2(x+3) = (2(x+3))³

Jak je vidět z předchozího příkladu, že skládání zobrazení obecně není komutativní. Lze však snadno ukázat, že je asociativní (tj. že nezáleží na pořadí uzávorkování), tedy že pro libovolná zobrazení f, g, h platí:. Důkaz získáme rozepsáním obou stran rovnosti podle definice složeného zobrazení. Pro libovolný prvek x tedy platí:  a . Obě strany jsou si tedy rovny a výrazy tak jsou ekvivalentní.

Operace: Buď  množina a  přirozené číslo. Zobrazení nazýváme n-ární algebraickou operací na množině . Číslo  nazýváme četností (aritou) operace. Pro n = 0 definujeme nulární operaci na  jako zvolení určitého prvku v množině  (čili výběr konstanty). Pro n = 1 hovoříme o unární operaci, pro n = 2 (nejběžnější případ) hovoříme o binární operaci, pro n = 3 o ternární, atd.

Příkladem unární operace (n = 1) v množině Z je (-a), kde a ∈ Z. Tato unární operace je převodem celého čísla a na opačné.  Příkladem binární operace f: Z ²  → Z na Z jsou operace sčítání, násobení, odčítání, … Tyto operace mají dva operandy a nejčastěji se píší v infixovém tvaru a₁ ⊕ a₂ , kde ⊕ zastupuje symbol obecné binární operace (+, º, -, …).