
Test o střední hodnotě při známém rozptylu (z-test pro jeden výběr)
Cílem  -testu pro jeden výběr je testovat hypotézu, zda data náhodného výběru pochází z rozdělení se stejnou střední hodnotou, jako je předpokládaná hodnota
-testu pro jeden výběr je testovat hypotézu, zda data náhodného výběru pochází z rozdělení se stejnou střední hodnotou, jako je předpokládaná hodnota  (konstanta). Vycházíme z realizace náhodného výběru o rozsahu
(konstanta). Vycházíme z realizace náhodného výběru o rozsahu 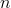 :
:  , o kterém předpokládáme, že pochází z normálního rozdělení. Předpokládáme tedy, že platí
, o kterém předpokládáme, že pochází z normálního rozdělení. Předpokládáme tedy, že platí  . Dále předpokládáme, že známe hodnotu parametru
. Dále předpokládáme, že známe hodnotu parametru 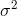 . Oba tyto předpoklady jsou velmi silné (a v biologické či klinické praxi téměř nereálné), neboť to znamená, že téměř přesně známe pravděpodobnostní chování náhodné veličiny
. Oba tyto předpoklady jsou velmi silné (a v biologické či klinické praxi téměř nereálné), neboť to znamená, že téměř přesně známe pravděpodobnostní chování náhodné veličiny 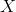 . Nulová hypotéza a příslušné alternativní hypotézy (oboustranná a jednostranné) pak mají následující tvar
. Nulová hypotéza a příslušné alternativní hypotézy (oboustranná a jednostranné) pak mají následující tvar
|
|
|
|
|
(1)
|
Výběrovou charakteristikou, která hraje v  -testu hlavní roli je samozřejmě výběrový průměr. Víme totiž, že za platnosti
-testu hlavní roli je samozřejmě výběrový průměr. Víme totiž, že za platnosti 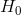 má výběrový průměr také normální rozdělení, z čehož plyne, že testová statistika
má výběrový průměr také normální rozdělení, z čehož plyne, že testová statistika 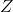 , kterou dostaneme z výběrového průměru standardizací, má standardizované normální rozdělení:
, kterou dostaneme z výběrového průměru standardizací, má standardizované normální rozdělení:
|
|
(2)
|
Pokud nulová hypotéza platí, statistika 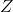 se bude realizovat v hodnotách běžných pro rozdělení
se bude realizovat v hodnotách běžných pro rozdělení 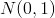 , a naopak, neplatí-li nulová hypotéza, statistika
, a naopak, neplatí-li nulová hypotéza, statistika 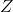 se bude realizovat v hodnotách, které nejsou pro standardizované normální rozdělení běžné. Nulovou hypotézu tak zamítáme na hladině významnosti
se bude realizovat v hodnotách, které nejsou pro standardizované normální rozdělení běžné. Nulovou hypotézu tak zamítáme na hladině významnosti 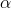 ve chvíli, kdy výsledná hodnota statistiky
ve chvíli, kdy výsledná hodnota statistiky 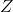 je větší (nebo menší, v závislosti na předem zvolené alternativě) než příslušný kvantil (kritická hodnota) rozdělení
je větší (nebo menší, v závislosti na předem zvolené alternativě) než příslušný kvantil (kritická hodnota) rozdělení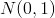 . Co znamená realizace statistiky v běžných hodnotách, bylo blíže rozebráno v kapitole 6, v případě oboustranného testu na hladině významnosti
. Co znamená realizace statistiky v běžných hodnotách, bylo blíže rozebráno v kapitole 6, v případě oboustranného testu na hladině významnosti 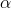 by se měla testová statistika
by se měla testová statistika 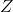 pohybovat mezi kvantily
pohybovat mezi kvantily 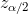 a
a  , což pro
, což pro 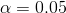 jsou hodnoty -1,96 a 1,96. Bude-li se statistika
jsou hodnoty -1,96 a 1,96. Bude-li se statistika 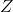 realizovat mimo tento interval, zamítáme nulovou hypotézu (na hladině významnosti
realizovat mimo tento interval, zamítáme nulovou hypotézu (na hladině významnosti 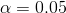 , samozřejmě). Vzhledem k symetrii kvantilů rozdělení
, samozřejmě). Vzhledem k symetrii kvantilů rozdělení 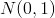 lze pravidlo pro zamítnutí
lze pravidlo pro zamítnutí 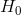 pro oboustrannou alternativu u
pro oboustrannou alternativu u  -testu zjednodušit na vyjádření, kdy absolutní hodnota statistiky
-testu zjednodušit na vyjádření, kdy absolutní hodnota statistiky 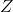 překročí hodnotu kvantilu
překročí hodnotu kvantilu  , tedy
, tedy  . Souhrnně jsou pravidla pro zamítnutí nulové hypotézy pro
. Souhrnně jsou pravidla pro zamítnutí nulové hypotézy pro  -test pro jeden výběr dle zvolené alternativy uvedena v tabulce 1.
-test pro jeden výběr dle zvolené alternativy uvedena v tabulce 1.
Tabulka 1: Pravidla pro zamítnutí 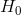 pro
pro  -test pro jeden výběr dle zvolené alternativy.
-test pro jeden výběr dle zvolené alternativy.
|
Alternativa
|
|
→ Zamítáme
|
|
|
Alternativa
|
|
→ Zamítáme
|
|
|
Alternativa
|
|
→ Zamítáme
|
|




