
Vlastnosti výběrového průměru
Nejen průměr, ale jakákoliv statistika je jako transformace náhodných veličin také náhodnou veličinou a má tudíž i vlastní rozdělení pravděpodobnosti. Vzhledem k tomu, že jednotlivé realizace náhodné veličiny vykazují variabilitu (popsanou směrodatnou odchylkou,
), pak i jednotlivé realizace statistiky nad různými náhodnými výběry vykazují variabilitu, která je úměrná
.
Co se týče výběrového průměru, má tento odhad dvě zajímavé vlastnosti, které jsou stěžejní nejen pro konstrukci intervalů spolehlivosti, ale i pro řadu dalších biostatistických úloh:
-
Rozdělení pravděpodobnosti výběrového průměru má tím menší rozptyl (variabilitu), čím více pozorování je v průměru zahrnuto, tedy čím větší je výběrový soubor (větší
). Jinými slovy, máme-li více informací, jsme schopni odhadovat s větší přesností. Tato vlastnost průměru plyne z vlastností rozptylu transformované náhodné veličiny.
-
Rozdělení pravděpodobnosti výběrového průměru se s rostoucí velikostí souboru (rostoucím n) přestává podobat rozdělení původní náhodné veličiny
a začíná se podobat rozdělení normálnímu. Tato vlastnost plyne z centrální limitní věty, která je klíčovým tvrzením teoretické statistiky.
Nejprve se věnujme rozptylu průměru jako transformované náhodné veličiny. Mějme posloupnost nezávislých náhodných veličin se stejným rozdělením pravděpodobnosti, které má konečnou střední hodnotu
a rozptyl
. Pak z pravidel pro výpočet rozptylu platí, že rozptyl výběrového průměru má tvar
|
|
(2) |
Pro praktické počítání je třeba pracovat se stejnými jednotkami, jako má původní náhodná veličina, což znamená vyjádřit i směrodatnou odchylku výběrového průměru:
|
|
(3) |
Výraz (3), tedy směrodatná odchylka výběrového průměru, se nejčastěji označuje pojmem standardní chyba (standard error), zkráceně značeno SE. Platí tedy
|
|
(4) |
Je velmi důležité si uvědomit, že směrodatná odchylka náhodné veličiny, tedy , je odrazem variability náhodné veličiny ve sledované populaci a souvisí tak s variabilitou biologického procesu (nelze ji tudíž ovlivnit). Na druhou stranu, směrodatná odchylka výběrového průměru, tedy standardní chyba
, je odrazem přesnosti výběrového průměru jako odhadu střední hodnoty náhodné veličiny a jako taková souvisí nejen s variabilitou biologického procesu, ale zejména s velikostí vzorku, která hodnotu standardní chyby ovlivňuje zásadním způsobem. Rozdíl mezi rozdělením pravděpodobnosti náhodné veličiny a výběrového průměru pro velikost výběru
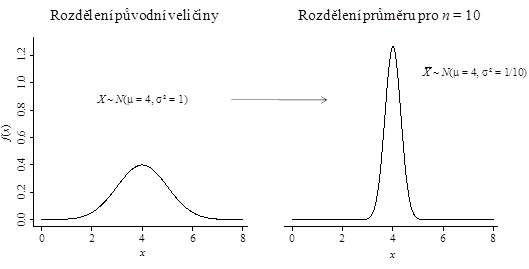
je uveden na obrázku 4.1. Z obrázku je vidět i to, že zatímco realizace náhodné veličiny z rozdělení N(4,1) v blízkosti čísla 5 je očekávatelná, realizace průměru deseti pozorování této veličiny v blízkosti čísla 5 je již velmi málo pravděpodobná.
 |
|
Obr. 4.1: Srovnání hustoty rozdělení původní veličiny a výběrového průměru pro n=10. |




