
Test o rozdílu středních hodnot dvou nezávislých výběrů při stejných rozptylech (t-test pro dva výběry)
Základním testem pro srovnávání středních hodnot dvou nezávislých výběrů je v biostatistice 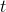 -test pro dva výběry, který testuje, zda náhodné výběry pochází z rozdělení se středními hodnotami, jejichž rozdíl je daná konstanta
-test pro dva výběry, který testuje, zda náhodné výběry pochází z rozdělení se středními hodnotami, jejichž rozdíl je daná konstanta  . Umožňuje nám tak posoudit, zda se hodnoty náhodné veličiny v jedné populaci statisticky významně liší od hodnot této náhodné veličiny v populaci druhé. Jedná se o parametrický test, jehož hlavním předpokladem je normalita rozdělení pravděpodobnosti obou náhodných výběrů. Máme-li realizaci prvního náhodného výběru o rozsahu
. Umožňuje nám tak posoudit, zda se hodnoty náhodné veličiny v jedné populaci statisticky významně liší od hodnot této náhodné veličiny v populaci druhé. Jedná se o parametrický test, jehož hlavním předpokladem je normalita rozdělení pravděpodobnosti obou náhodných výběrů. Máme-li realizaci prvního náhodného výběru o rozsahu 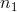 :
:  , a na ní nezávislou realizaci druhého náhodného výběru o rozsahu
, a na ní nezávislou realizaci druhého náhodného výběru o rozsahu 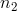 :
:  , předpokládáme, že jak realizace
, předpokládáme, že jak realizace 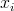 , tak realizace
, tak realizace  pocházejí z normálního rozdělení, tedy že platí
pocházejí z normálního rozdělení, tedy že platí  ,
,  , a
, a  ,
,  . Nulová hypotéza, předpokládající rozdíl mezi středními hodnotami roven
. Nulová hypotéza, předpokládající rozdíl mezi středními hodnotami roven  (nejčastěji volíme
(nejčastěji volíme  = 0), a příslušné alternativní hypotézy (oboustranná a jednostranné) mají tvar
= 0), a příslušné alternativní hypotézy (oboustranná a jednostranné) mají tvar
|
|
|
|
|
(17)
|
Je důležité si uvědomit, že jsme opět v situaci, kdy neznáme skutečnou hodnotu parametru 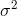 , pouze předpokládáme, že je stejná pro oba výběry. Tento neznámý parametr odhadujeme pomocí váženého průměru odhadů rozptylu (výběrových rozptylů) v jednotlivých skupinách,
, pouze předpokládáme, že je stejná pro oba výběry. Tento neznámý parametr odhadujeme pomocí váženého průměru odhadů rozptylu (výběrových rozptylů) v jednotlivých skupinách, 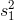 a
a  :
:
|
|
(18)
|
Z vlastností normálního rozdělení pravděpodobnosti plyne, že rozdíl průměrů normálních náhodných veličin 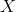 a
a 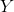 je také normální náhodná veličina. Vzhledem k neznámému parametru
je také normální náhodná veličina. Vzhledem k neznámému parametru 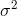 nelze použít pro testování statistiku s normálním rozdělením pravděpodobnosti, proto obdobně jako v případě
nelze použít pro testování statistiku s normálním rozdělením pravděpodobnosti, proto obdobně jako v případě 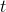 -testu pro jeden výběr i zde hraje roli testové statistiky statistika
-testu pro jeden výběr i zde hraje roli testové statistiky statistika 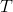 se Studentovým
se Studentovým 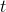 rozdělením (s
rozdělením (s  stupni volnosti). Pro dva výběry je statistika
stupni volnosti). Pro dva výběry je statistika 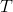 definována jako
definována jako
|
|
(19)
|
Nulovou hypotézu opět zamítáme na hladině významnosti 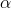 ve chvíli, kdy realizace statistiky
ve chvíli, kdy realizace statistiky 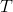 překročí určitou hranici, kterou je kvantil Studentova rozdělení
překročí určitou hranici, kterou je kvantil Studentova rozdělení  příslušný hladině
příslušný hladině 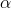 a zvolené alternativě. Souhrn pravidel pro zamítnutí nulové hypotézy platných pro
a zvolené alternativě. Souhrn pravidel pro zamítnutí nulové hypotézy platných pro 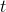 -test pro dva výběry dle zvolené alternativy je uveden v tabulce 5. Kromě pravidel pro rozhodnutí o platnosti
-test pro dva výběry dle zvolené alternativy je uveden v tabulce 5. Kromě pravidel pro rozhodnutí o platnosti 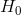 je třeba mít na paměti, že použití
je třeba mít na paměti, že použití 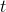 -testu pro dva výběry má dva velmi silné předpoklady, kterým bychom měli před výpočtem vždy věnovat adekvátní pozornost. Těmito předpoklady jsou
-testu pro dva výběry má dva velmi silné předpoklady, kterým bychom měli před výpočtem vždy věnovat adekvátní pozornost. Těmito předpoklady jsou
-
Normalita pozorovaných hodnot, a to v rámci obou náhodných výběrů. Předpoklad normality musíme předem otestovat adekvátním testem nebo alespoň graficky ověřit pomocí dostupných vizualizačních nástrojů (histogram, krabicový graf).
-
Homogenní (stejný) rozptyl náhodné veličiny, opět v rámci obou srovnávaných výběrů. Předpoklad homogenity rozptylu lze stejně jako normalitu testovat příslušným statistickým testem (tomuto tématu je věnována část 3.2 o tzv.
-testu), možné je i grafické ověření pomocí výše zmíněných nástrojů (histogram, krabicový graf).
Tabulka 5: Pravidla pro zamítnutí 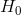 pro
pro 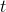 -test pro dva výběry dle zvolené alternativy.
-test pro dva výběry dle zvolené alternativy.
|
Alternativa
|
|
→ Zamítáme
|
|
|
Alternativa
|
|
→ Zamítáme
|
|
|
Alternativa
|
|
→ Zamítáme
|
|
Příklad 3. Uvažujme léčbu pacientů se špatně kontrolovanou hypertenzí, pro kterou je dostupná léčba tzv. ACE inhibitory (ACE-I) a antagonisty pro angiotensin II receptor (AIIA). Účinnost léčby ACE-I u pacientů se špatně kontrolovanou hypertenzí reprezentujeme náhodnou veličinou 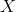 , zatímco účinnost léčby AIIA u těchto pacientů popíšeme náhodnou veličinou
, zatímco účinnost léčby AIIA u těchto pacientů popíšeme náhodnou veličinou 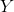 . Nulová hypotéza pak vyjadřuje stejný účinek obou léků (ve smyslu střední hodnoty) na snížení diastolického tlaku (TKd) těchto pacientů měřený v milimetrech rtuti po šesti měsících od zahájení léčby. Tedy
. Nulová hypotéza pak vyjadřuje stejný účinek obou léků (ve smyslu střední hodnoty) na snížení diastolického tlaku (TKd) těchto pacientů měřený v milimetrech rtuti po šesti měsících od zahájení léčby. Tedy
|
|
|
(20)
|
U pacientů léčených ACE-I (skupina 1), respektive AIIA (skupina 2), byly pozorovány následující výběrové charakteristiky:
|
|
|
(21)
|
Dále byl na základě hodnot 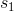 a
a  vypočten vážený odhad parametru
vypočten vážený odhad parametru 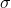 ,
,  =9.88. Víme, že za platnosti
=9.88. Víme, že za platnosti 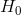 platí
platí  , což znamená, že můžeme pro testování použít statistiku
, což znamená, že můžeme pro testování použít statistiku 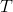 definovanou v (22). Po dosazení získáme
definovanou v (22). Po dosazení získáme
|
|
(22)
|
Absolutní hodnotu výsledné realizace testové statistiky srovnáme s kvantilem Studentova 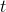 rozdělení s 3811 stupni volnosti (vzhledem k platnosti centrální limitní věty zde již můžeme použít kvantil rozdělení
rozdělení s 3811 stupni volnosti (vzhledem k platnosti centrální limitní věty zde již můžeme použít kvantil rozdělení 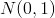 ). Absolutní hodnota testové statistiky je menší než hodnota kvantilu
). Absolutní hodnota testové statistiky je menší než hodnota kvantilu  = 1,96 a tedy nulovou hypotézu nezamítáme. Závěrem tedy lze říci, že na hladině významnosti
= 1,96 a tedy nulovou hypotézu nezamítáme. Závěrem tedy lze říci, že na hladině významnosti 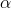 = 0,05 nelze prokázat rozdíl mezi léčbou ACE-I a AIIA vzhledem ke snížení diastolického tlaku u pacientů se špatně kontrolovanou hypertenzí.
= 0,05 nelze prokázat rozdíl mezi léčbou ACE-I a AIIA vzhledem ke snížení diastolického tlaku u pacientů se špatně kontrolovanou hypertenzí.




