Spojitý prediktor

V kapitole Motivace jsme si na příkladu již ukázali modelování jednoduché závislosti výsledku na spojité proměnné. Závislost je v takovém případě vyjádřena regresní přímkou – s každou jednotkou prediktoru narůstá (nebo klesá) očekávaná hodnota výsledkové proměnné o hodnotu regresního koeficientu – sklonu regresní přímky. V následujícím zápisu regresního modelu je tímto koeficientem β₁.

Obrázek 2.3 ukazuje závislost hodnoty indexu tělesné hmotnosti (BMI) na procentuálním vyjádření podílu tukové tkáně. Závislost je v souladu s definovaným modelem vyjádřena přímkou.

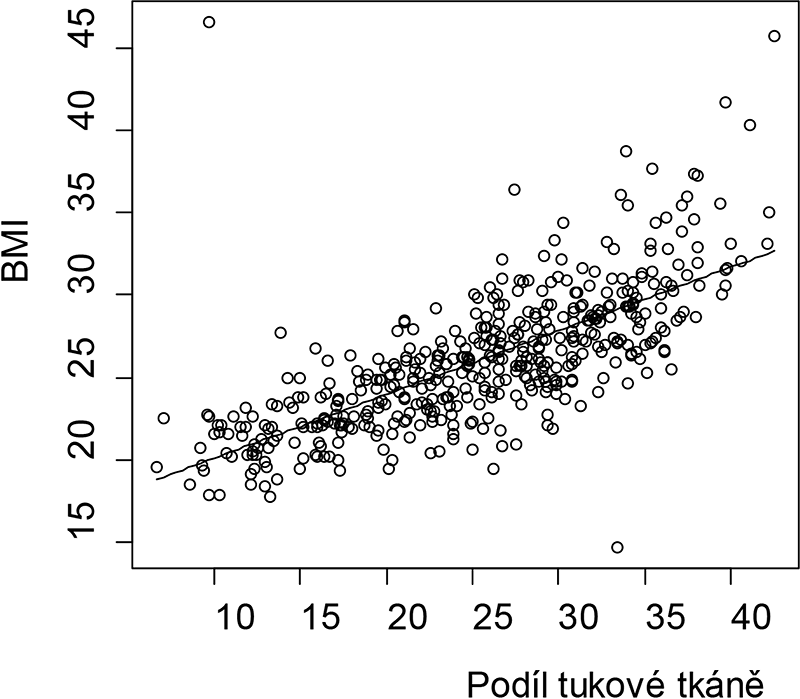
Obr. 2.3: Závislost indexu tělesné hmotnosti (BMI) na podílu tukové tkáně: lineární model.

V praxi se setkáme i se situací, kdy chceme modelovat závislost výsledku na spojité proměnné, lineární model reprezentovaný přímkou však nemusí být adekvátní. Regresní modelování umožňuje snadno modelovat regresní křivku polynomem vyššího stupně. Ukážeme si modelování kvadratické závislosti. V takovém případě zahrneme do matice plánu další sloupec s hodnotami druhé mocniny původní proměnné. Na obrázku 2.4 je znázorněna obdobná závislost jako na předchozím obrázku, nyní však již s nelineárním kvadratickým modelem.

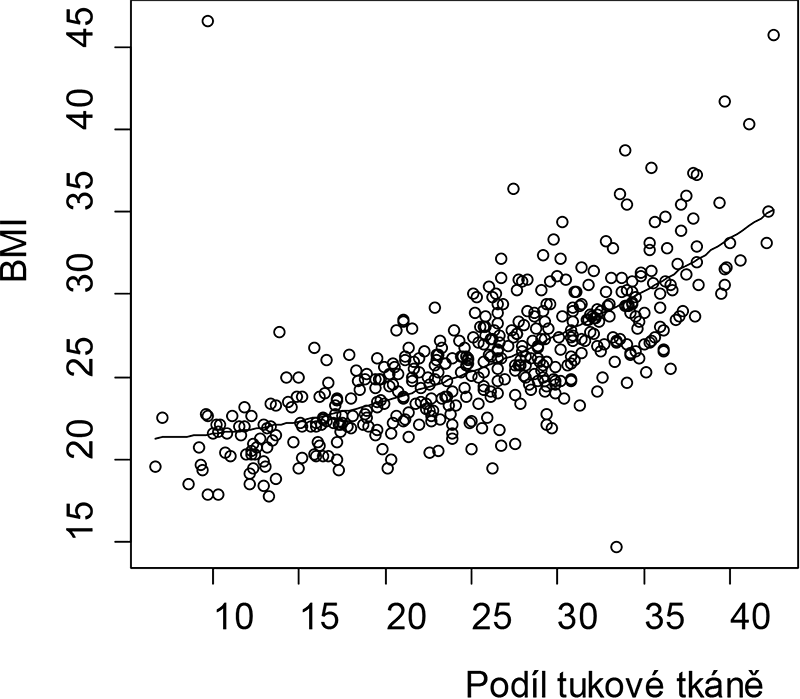
Obr. 2.4: Závislost indexu tělesné hmotnosti (BMI) na podílu tukové tkáně: kvadratický model.