Lineární regresní model

Předpokládejme na chvilku, že existuje pro všechna pozorování přesný vztah mezi dvěma (nenáhodnými) veličinami y (výsledek) a x (prediktor):

Takto definovaný vztah mezi veličinami však na reálných datech (zejména z biologie nebo medicíny) v praxi pozorujeme stěží. Pro regresní modelování se proto využívá následujícího vztahu, který v sobě již zahrnuje náhodnou veličinu ε (reziduum) reprezentující odchylku od uvedeného ideálního vztahu. Y označuje výsledek (náhodnou veličinu), x označuje prediktor (nenáhodnou, přesně změřenou veličinu). Předpokládejme tedy, že pro jednotlivá pozorování (např. pacienty, lokality, apod.) číslované prostřednictvím indexu i od 1 do n (celkový počet pozorování) platí:

(2.1)

O reziduích budeme předpokládat, že jsou

• nesystematické – střední hodnota reziduí je rovna 0: pro i = 1,...,n
• homogenní v rozptylu – rozptyl reziduí je pro všechna pozorování stejný: pro i = 1,...,n
• jsou vzájemně nekorelované:  pro i ≠ j; i, j = 1,...,n
   

Pro jeden prediktor x se regresní koeficienty značí β₀ a β₁, jedná se o zmíněný absolutní člen a směrnici regresní přímky. Uvedený vztah lze jednoduše rozšířit na větší počet (p) prediktorů (pak máme celkem k = p + 1 parametrů včetně β₀, absolutního členu). Dostáváme definici vícenásobného regresního modelu (multiple regression):

(2.2)

Rozepsáno do vztahů pro očekávané hodnoty (predikce) jednotlivých pozorování i = 1,...,n:

.

.

Tuto soustavu vztahů můžeme zapsat jako následující vztah využívající násobení matic:

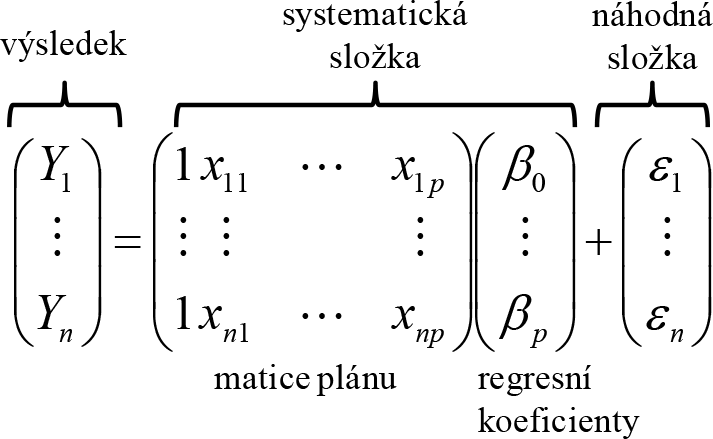
Vektor výsledků, matici plánu, vektor regresních koeficientů a vektor reziduí označíme po řadě Y, X, β a ε. Maticový zápis regresních rovnic nám umožní zjednodušit definice potřebných statistik.

(2.3)