Definice Poissonova regresního modelu
Cílem Poissonova regresního modelu je modelování proměnných s poissonovsky rozděleným výsledkem. Poissonovo rozdělení je diskrétní rozdělení, které popisuje počet výskytů sledované události na danou jednotku (času, plochy, objemu), když se tyto události vyskytují vzájemně nezávisle s konstantní intenzitou (jediný parametr ).
Poissonovo rozdělení má tuto pravděpodobnostní funkci:
Střední hodnota a rozptyl jsou dány jediným parametrem .
Abychom Poissonův regresní model nadefinovali, uvažujme jedno pozorování (např. jedna Petriho miska, na které počítáme buňky, jeden rok, kdy zaznamenáváme pacienty nově diagnostikované s nádorovým onemocněním). Toto pozorování je rozděleno poissonovsky:
Srovnejme lineární regresi (vlevo) s Poissonovou regresí (vpravo)
|
modelujeme spojitý výsledek
hodnota parametru (střední hodnoty) je rovna lineárním prediktoru
|
modelujeme poissonovský výsledek
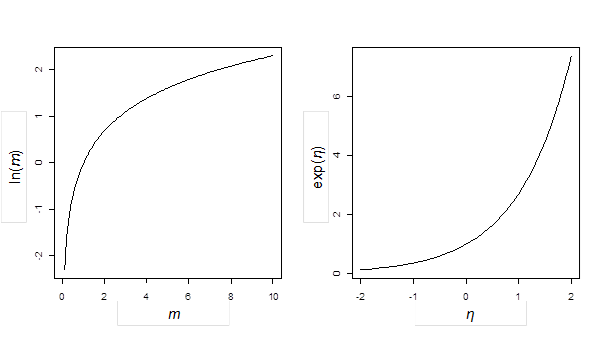
hodnota parametru (střední hodnoty) je rovna transformovanému prediktoru: hodnota lineárního prediktoru odpovídá střední hodnotě transformované přirozeným logaritmem
|
Stejně jako u logistické regrese používáme linkovací funkci, která nám pomáhá modelovat pomocí lineárního prediktoru (který nabývá různých hodnot na reálné ose) výsledek, který by měl být určitě pozitivní. Takovou funkcí je přirozený logaritmus (obr. 4).