Biodiverzita z matematického hlediska

Z hlediska matematického pozadí výpočtů souvisí analýza diverzity s entropií a informační teorií. Jednotlivé taxony, geny nebo jakékoliv součásti určitého systému představují jednotky informace. Pojem entropie lze chápat jako míru „neuspořádanosti“ zkoumaného systému. Tento pojem zavedl v roce 1865 německý fyzik Rudolf Clausius (1822-1888) v souvislosti s termodynamickými zákony a z hlediska teorie informace jej popsal Claude Elwood Shannon (1916-2001). 

Neustálý růst složitosti je podmíněn růstem entropie. Tuto situaci si lze graficky představit jako pyramidu, na jejíž špičce je nula: začátek všeho, nulová entropie, žádný pohyb, žádný čas. Od této chvíle se budují stále složitější struktury a postupujeme směrem dolů ke stavu s vyšší entropií. Pyramida se neustále rozšiřuje, každý následující stav je ovlivněn předchozím stavem. Na určitém místě, relativně blízko špičce, vznikla hmota vesmíru, na jiném daleko níže je vznik prvních živých jednobuněčných organismů a ještě níž člověk, přičemž entropie, tedy složitost systému, stále narůstá (obr. 1.2). Entropie je jedním ze základních a nejdůležitějších pojmů ve fyzice, matematice, teorii pravděpodobnosti a informace a v mnoha dalších oblastech vědy teoretické i aplikované. Setkáváme se s ní všude tam, kde hovoříme o pravděpodobnosti možných stavů daného systému či soustavy.

Chápeme-li entropii jako neurčitost systému, můžeme pojem entropie nahradit pojmem diverzita, a pokud naše zkoumané systémy jsou biologické, lze mluvit o biodivezitě. Z tohoto hlediska může být biodiverzita chápána jako „neuspořádanost“ biologických systémů.

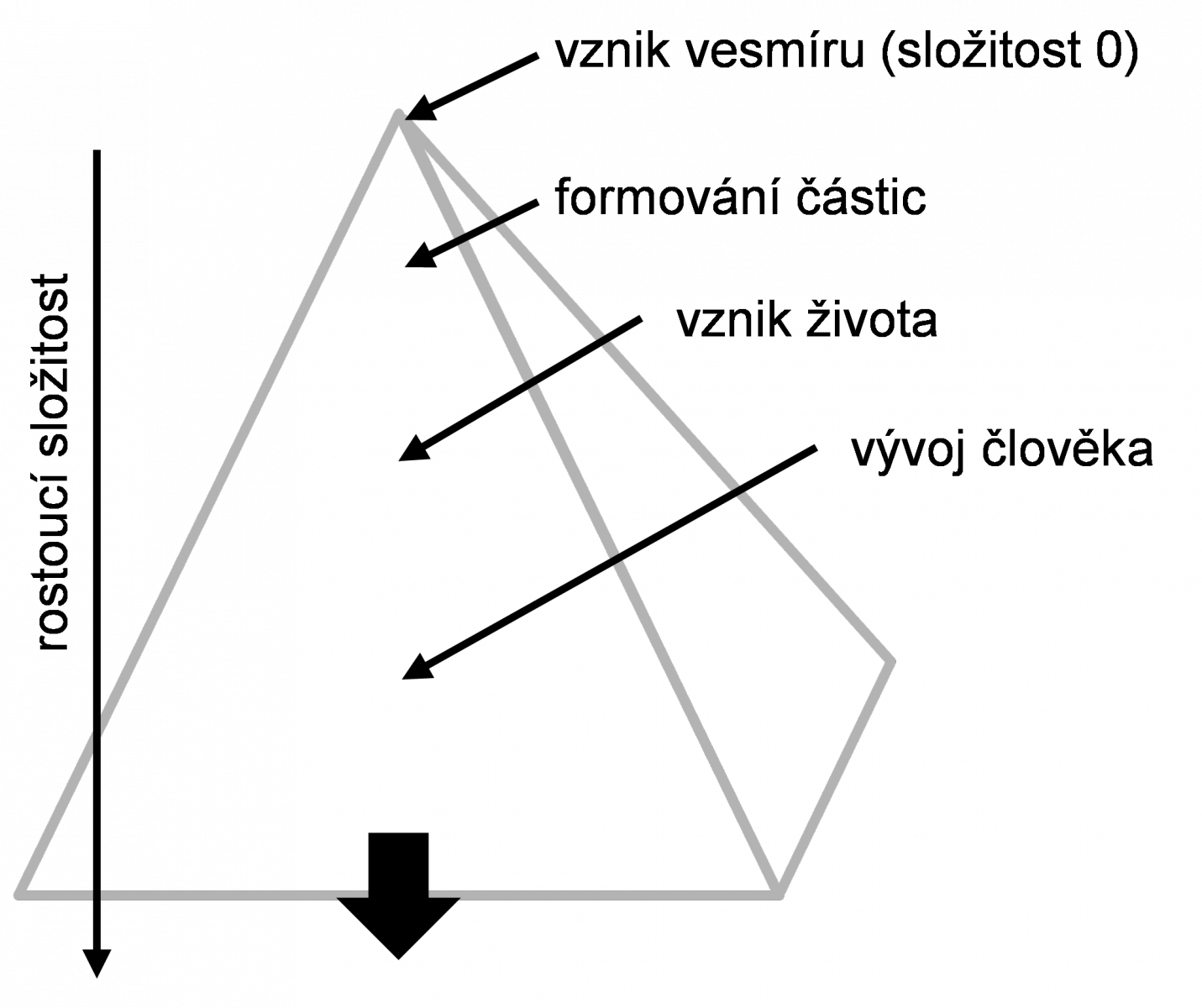Obr. 1.2: Postupný nárůst entropie  od vzniku vesmíru