Binární koeficienty podobnosti
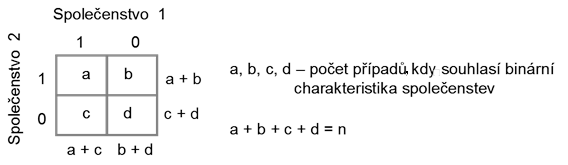
Binární metriky počítají pouze s přítomností nebo absencí taxonů. Dále je můžeme rozdělit na symetrické a asymetrické. Symetrické metriky nerozlišují mezi případem 1–1 a 0–0, obě události mají stejnou váhu. Asymetrické koeficienty rozlišují mezi 1–1 a 0–0, přičemž existuje mnoho postupů, jak spočítat míru asociace mezi druhy založené na binárních datech. Tyto koeficienty jsou založené na 2 × 2 frekvenční tabulce (Obr. 8.3:).
|
|
|
Obr. 8.3: Výpočet binárních metrik podobnosti na základě 2 × 2 frekvenční tabulky |
V případě lineární odpovědi organismů na prostředí je možné využít symetrické binární koeficienty.
Jednoduchý srovnávací koeficient, kdy metodou pro výpočet podobnosti mezi dvěma objekty je podíl počtu deskriptorů, které kódují objekt stejně a celkového počtu deskriptorů.
|
|
(1.1) |
kde a
jsou srovnávaná společenstva,
je počet současných výskytů,
počet současných nevýskytů a
počet všech taxonů ve srovnávaných společenstvech. Při použití tohoto koeficientu předpokládáme, že není rozdíl mezi nastáním 0 a 1 u deskriptorů.
Rogersův a Tanimotův koeficient dává větší váhu rozdílům než podobnostem:
|
|
(1.2) |
kde a
jsou srovnávaná společenstva,
je počet současných výskytů,
počet současných nevýskytů
,
počet neshodujících se taxonů ve srovnávaných společenstvech. Obdobné indexy, které stejně jako (1.2) snižují vliv dvojité nuly, byly navrženy Sneathem a Sokalem:
|
|
(1.3) |
tento koeficient dává dvakrát větší váhu shodným deskriptorům než rozdílným.
|
|
(1.4) |
porovnává shody a rozdíly prostým podílem v měřítku jdoucím od 0 do nekonečna.
|
|
(1.5) |
porovnává shodné deskriptory se součty okrajů tabulky.
|
|
(1.6) |
je vytvořen z geometrických průměrů členů vztahujících se k a
.
Pro eliminaci vlivu problému dvojité nuly jsou využity asymetrické binární koeficienty. Nejznámější z nich je Jaccardův koeficient:
|
|
(1.7) |
kde a
jsou srovnávaná společenstva,
je počet současných výskytů a
,
je počet neshodujících se taxonů ve srovnávaných společenstvech.
Sørensenův koeficient jako varianta předchozího koeficientu dává dvojnásobnou váhu dvojitým prezencím
|
|
(1.8) |
protože se může zdát, že přítomnost druhů je více informativní než jejich absence, která může být způsobena různými faktory a nemusí nutně odrážet rozdílnost prostředí. Prezence druhu na obou lokalitách je silným ukazatelem jejich podobnosti. ((1.7) je monotónní k ((1.8), proto podobnost pro dvě dvojice objektů vypočítaná podle ((1.7) bude podobná stejnému výpočtu ((1.8). Oba koeficienty se liší pouze v měřítku. Jiná varianta tohoto koeficientu dává duplicitním prezencím trojnásobnou váhu:
|
|
(1.9) |
Následující koeficient byl navržen jako doplněk Rogersova a Tanimotova koeficientu a dává dvojnásobnou váhu rozdílům ve jmenovateli.
|
|
(1.10) |
Russelův a Raův koeficient umožňuje porovnání počtu duplicitních prezencí (v čitateli) proti celkovému počtu druhů, nalezených na všech lokalitách, zahrnujícím druhy, které chybějí () na obou uvažovaných lokalitách.
|
|
(1.11) |
Kulczynski nabízí koeficient porovnávající duplicitní prezence s diferencemi:
|
|
(1.12) |
Mezi svými koeficienty pro presence/absence dat zmiňují Sneath a Sokal tuto verzi koeficientu:
|
|
(1.13) |
kde jsou duplicitní prezence srovnávány se součty okrajů tabulky a
.
Ochia použil obdobně jako míru podobnosti geometrický průměr poměrů a k počtu druhů na každé lokalitě, tj. se součty okrajů tabulky a
:
|
|
(1.14) |
Faith popsal koeficient, kde je neshoda (přítomnost na jedné a absence na druhé lokalitě) vážena proti duplicitní prezenci. Hodnota klesá s růstem počtem dvojí nepřítomnosti.
|
|
(1.15) |
V biogeografii je pro asociaci taxonů na bázi společného výskytu na lokalitách často používán Baroniův-Urbaniův a Buserův index podobnosti, který lze zapsat jako:
|
|
(1.16) |
kde a je počet lokalit, ve kterých je přítomný druh A, je počet lokalit, ve kterých je přítomný druh B,
počet lokalit, ve kterých jsou přítomny oba druhy A i B a
je počet lokalit, ve kterých není přítomen ani jeden z porovnávaných druhů A a B. Na rozdíl od Jaccardova indexu, který nebere v úvahu společné absence obou porovnávaných druhů (
), se u tohoto indexu uvádí, že společná absence druhů na lokalitách je důležitá, neboť může mít ekologickou či historickou příčinu a proto by neměla být opomíjena. Baroniův-Urbaniův a Buserův index dává větší významnost společné přítomnosti tím, že společné prezence jsou násobeny společnými absencemi. Tímto se eliminuje chybný výsledek, že dva druhy jsou svým rozšířením považovány za podobné pouze kvůli společným absencím.