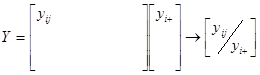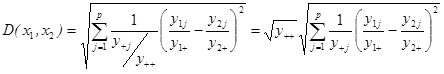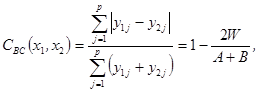Kvantitativní koeficienty podobnosti a vzdálenosti společenstev
V případě použití abundancí taxonů je opět nutné rozhodnout, zda bude použit některý koeficient pro data na krátkém environmentálním gradientu, tedy bez problému dvojité nuly, nebo koeficient řešící tento problém na dlouhém environmentálním gradientu.
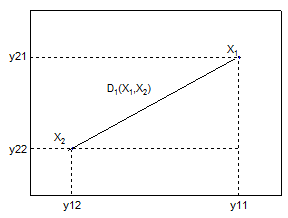
V případě nepřítomnosti problému dvojité nuly je možné využít základní euklidovskou metriku, která počítá vzdálenost objektů obdobně, jako Pythagorova věta počítá přeponu pravoúhlého trojúhelníku (Obr. 8.4). Metoda je citlivá na rozdílný rozsah hodnot vstupujících proměnných (vhodným řešením může být standardizace) a problém dvojité nuly. Nemá horní hranici hodnot a standardně je vyjádřena ve formě vzdálenosti.
|
|
(1.17) |
kde a
jsou srovnávaná společenstva,
je počet taxonů ve společenstvu a
a
jejich abundance ve společenstvech.
|
|
|
Obr. 8.4: Princip výpočtu euklidovské vzdálenosti |
Její variantou je manhattanská vzdálenost, kdy jde o součet rozdílů jednotlivých parametrů popisujících objekty.
|
|
(1.18) |
Modifikací euklidovské vzdálenosti je takzvaná tětivová vzdálenost (chord distance). Odstraňuje problém dvojité nuly a vliv rozdílného počtu jedinců druhů ve vzorcích při výpočtu euklidovské vzdálenosti. Její maximální hodnota je 1 a minimum 0. Při výpočtu počítá pouze s poměry druhů v rámci jednotlivých vzorků. Jde vlastně o euklidovskou vzdálenost počítanou pro vektory vzorků standardizované na délku 1, nebo je možný přímý výpočet už zahrnující standardizaci.
|
|
(1.19) |
Vnitřní část výpočtu je vlastně cosinus úhlu svíraného vektory, zápis vzorce je možný i v této formě.
|
|
(1.20) |
Whittakerův asociační index je dobře použitelný pro data abundancí, každý druh je nejprve transformován ve svůj podíl ve společenstvu, následný výpočet je opět jako u manhattanské vzdálenosti.
|
|
(1.21) |
Jeho hodnota je 0 v případě identických proporcí druhů. Stejný výsledek lze získat i jako součet nejmenších podílů v rámci obou vzorků.
|
|
(1.22) |
Canberrská vzdálenost je opět varianta manhattanské vzdálenosti (před výpočtem musí být odstraněn problém dvojité přítomnosti). Stejný rozdíl mezi početnými druhy ovlivňuje vzdálenost méně než mezi druhy vzácnějšími.
|
|
(1.23) |
metrika náleží do skupiny metrik založených na
pro výpočet vzdáleností odběrů založených na abundancích druhů nebo jiných frekvenčních datech (nejsou přípustné žádné záporné hodnoty). Data původní matice abundancí/frekvencí Y jsou nejprve přepočítána do matice poměrných frekvencí (součty frekvencí v řádcích (odběry) jsou rovny 1). Jako dodatečné charakteristiky uplatňované při výpočtu jsou spočteny součty řádků
a sloupců
celé matice
odběrů
druhů.
|
|
(1.24) |
Výpočet odstraňuje problém dvojité nepřítomnosti. Nejjednodušším výpočtem je obdoba euklidovské vzdálenosti.
|
|
(1.25) |
která je dále vážena součty jednotlivých druhů
|
|
(1.26) |
Index je možné využít i pro měření vzdálenosti mezi druhy na základě jejich rozložení v odběrech.
relativní metrika je podobná
metrice, ale vážení je prováděno relativní četností řádku v matici místo jeho absolutního součtu, při výpočtu se užívá parametr
(celkový součet matice). Je využívána také při výpočtu vztahů řádků a sloupců kontingenční tabulky.
|
|
(1.27) |
V případě analýz na dlouhém environmentálním gradientu jsou v ekologii dlouhodobě etablovány následující koeficienty podobnosti:
Brayův–Curtisův koeficient - tento koeficient porovnává dvě společenstva z hlediska minimální abundance u každého druhu.
|
|
(1.28) |
kde W je součet minimálních abundancí druhu, A a B je součet abundancí jednotlivých společenstev.
Často je používána také kvantitativní varianta Sørensenova koeficientu
|
|
(1.29) |
kde a
jsou celkové počty jedinců ve společenstvu na lokalitách A a B a
je suma abundancí druhů, pokud se druh vyskytuje v obou společenstvech.
Dalším významným koeficientem je Morisitův – Hornův index
|
|
(1.30) |
kde je počet jedinců druhu ve společenstvu A a
počet jedinců druhu i ve společenstvu A (obdobně platí pro společenstvo B).