Statistický test

Testování hypotéz probíhá na základě pozorovaných hodnot náhodné veličiny (dat) a statistického testu, který odpovídá testované nulové hypotéze a který nám umožní ověřit její platnost. Statistický test je reprezentován tzv. testovou statistikou (test statistic), což je transformace pozorovaných hodnot (náhodného výběru) pocházejících z určitého rozdělení pravděpodobnosti.  To znamená, že sama testová statistika je také náhodnou veličinou a má nějaké rozdělení pravděpodobnosti. Rozdělení pravděpodobnosti testové statistiky za platnosti nulové hypotézy, H₀, lze najít v anglické literatuře pod pojmem null distribution.

Provedení testu pak probíhá následujícím způsobem: na základě dat vypočítáme hodnotu testové statistiky, kterou srovnáme s kvantilem, často označovaným jako tzv. kritická hodnota, jejího rozdělení pravděpodobnosti odpovídajícím zvolené hladině významnosti testu α. Pohybuje-li se hodnota realizace testové statistiky v rozmezí běžných hodnot daných rozdělením pravděpodobnosti testové statistiky za platnosti nulové hypotézy, H₀, tedy hodnota realizace nepřekračuje kritickou hodnotu, pak nulovou hypotézu nezamítáme. Naopak, představuje-li hodnota realizace testové statistiky extrémnější (méně pravděpodobnou) hodnotu v rámci rozdělení pravděpodobnosti odpovídajícího nulové hypotéze, než je kritická hodnota (kvantil rozdělení) odpovídající zvolenému riziku α, pak nulovou hypotézu zamítáme. Jinými slovy hodně pravděpodobné nebo běžné hodnoty realizace testové statistiky v rámci rozdělení pravděpodobnosti testové statistiky za platnosti nulové hypotézy potvrzují platnost statistické hypotézy, zatímco málo pravděpodobné až extrémní hodnoty realizace testové statistiky do tohoto rozdělení zřejmě nepatří, což naznačuje neplatnost nulové hypotézy. V souvislosti se zvolenou alternativní hypotézou riziko špatného rozhodnutí, které podstupujeme, buď rovnoměrně rozdělujeme na obě extrémní varianty výsledku (extrémně nízké i vysoké hodnoty testové statistiky) a jedná se tak o tzv. oboustranný test, nebo uvažujeme pouze jednu extrémní variantu výsledku (buď extrémně nízké, nebo extrémně vysoké hodnoty testové statistiky) a jedná se tak o tzv. jednostranný test. Ukázka kritických hodnot pro případ, kdy uvažujeme testovou statistiku se standardizovaným normálním rozdělením, hladinu významnosti α = 0,05 a oboustrannou i jednostrannou alternativu, je uvedena na obrázku 6.1. Zde jsou pro oboustrannou alternativu kritickými hodnotami kvantily z_α/2 a z_1-α/2, tedy kvantily z_0,025 a z_0,975 (čísla -1,96 a 1,96), standardizovaného normálního rozdělení N(0,1), zatímco pro jednostrannou alternativu je kritickou hodnotou kvantil z_1-α, tedy kvantil z_0,95 (číslo 1,64).

Fakticky realizace testové statistiky v oblasti málo pravděpodobných hodnot rozdělení pravděpodobnosti za platnosti nulové hypotézy znamená, že nastala jedna ze dvou situací:

1. H₀ platí a my jsme pozorovali málo pravděpodobný jev
2. H₀ neplatí

Pozorování málo pravděpodobných jevů máme ošetřeno rizikem α (pravděpodobností chyby I. druhu), jinými slovy málo pravděpodobné jevy jsou součástí našeho rizika, proto se v takovém případě kloníme k druhé možnosti a zamítáme H₀. Zamítáme-li nulovou hypotézu, je vždy nutné tuto informaci doplnit právě hodnotou α, tedy informací, na jaké hladině významnosti jsme test prováděli.

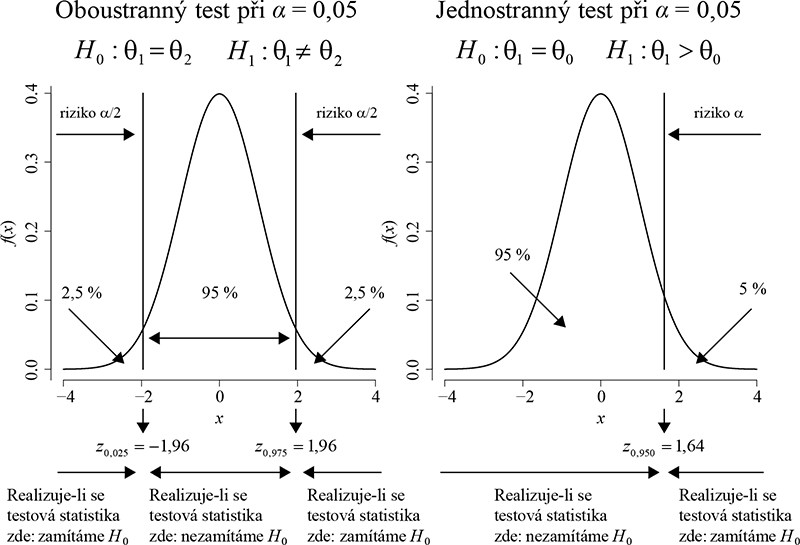
Obr. 6.1: Znázornění kritických hodnot pro oboustranný a jednostranný test vzhledem k riziku α.

 

Příklad 6.1. Při populačním epidemiologickém průzkumu bylo zjištěno, že průměrný objem prostaty u mužů je 32,73 ml (s výběrovou směrodatnou odchylkou s = 18,12 ml). Na hladině významnosti testu α = 0,05 chceme ověřit, jestli se objem prostaty u mužů nad 70 let liší od celé populace. Máme náhodný výběr o velikosti n = 100, kde byl naměřen výběrový průměr objemu prostaty 36,60 ml. Označme objem prostaty u mužů nad 70 let jako náhodnou veličinu X, střední hodnotu této veličiny symbolem µ a předpokládejme, že nemáme apriorní znalost toho, zda starší muži mají prostatu spíše větší nebo menší než mužská populace jako celek. Nulová hypotéza a příslušná oboustranná alternativní hypotéza pak mají následující tvar:

 

(6.7)

Předpokládejme, že jsme v situaci, kdy víme, že výběrová směrodatná odchylka, s, zjištěná v populační studii odpovídá skutečné směrodatné odchylce σ. Z vlastností výběrového průměru za platnosti nulové hypotézy platí, že

(6.8)

Dále z centrální limitní věty víme, že platí-li (6.8) platí i následující:

(6.9)

Pokud tedy výběrový průměr náhodné veličiny X patří do rozdělení , neměla by realizace statistiky Z být vzhledem ke standardizovanému normálnímu rozdělení nijak extrémní. Na základě pozorovaných hodnot vypočteme realizaci testové statistiky Z jako

(6.10)

Nyní je otázkou, můžeme zamítnout nulovou hypotézu na hladině významnosti testu α = 0,05 nebo ne? Uvážíme-li zvolené riziko α = 0,05, pak by se měla realizace testové statistiky Z v 95 % případů pohybovat mezi kvantily z_α/2 a z_1-α/2, tedy hodnotami -1,96 a 1,96 (viz také obrázek 6.1 vlevo). V ideálním případě (z hlediska nulové hypotézy), pokud bychom dospěli u mužů starších 70 let ke stejnému výběrovému průměru jako v případě populační studie, by hodnota testové statistiky byla rovna nule, což je samozřejmě číslo mezi hodnotami -1,96 a 1,96. V našem případě ale platí

(6.11)

a číslo 2,14 tak představuje extrémnější (méně pravděpodobnou) hodnotu v rámci rozdělení pravděpodobnosti odpovídajícího nulové hypotéze, než je kritická hodnota, což naznačuje neplatnost nulové hypotézy. Na hladině významnosti α = 0,05 tak zamítáme nulovou hypotézu o rovnosti objemu prostaty u mužů nad 70 let populační hodnotě 32,73 ml, protože výsledná hodnota testové statistiky je větší než příslušný kvantil (kritická hodnota) standardizovaného normálního rozdělení N(0,1).