
Normální rozdělení pravděpodobnosti
Znalost rozdělení pravděpodobnosti, kterým se řídí námi studovaná náhodná veličina, není nezbytná. Existují totiž statistické metody, standardně jsou označovány jako neparametrické metody (non-parametric methods), které nevyžadují specifikaci konkrétního rozdělení pozorovaných hodnot. Na druhou stranu, tato znalost, kterou vyžadují tzv. parametrické metody (parametric methods), je vždy výhodná, neboť použití parametrických metod je většinou jednodušší a při korektně specifikovaném rozdělení i přesnější. Podmínka korektní specifikace je však nesmírně důležitá. Pokud totiž předpokládáme pravděpodobnostní chování studované cílové populace dle určitého rozdělení, ale ve skutečnosti tento předpoklad splněn není, je špatně specifikace celého statistického modelu, což vede k zavádějícím výsledkům a neinterpretovatelným závěrům.
Normální rozdělení pravděpodobnosti (normal probability distribution) je spojité rozdělení pravděpodobnosti, které popisuje celou řadu veličin, jejichž hodnoty se symetricky shlukují kolem střední hodnoty a vytvářejí tak charakteristický tvar hustoty pravděpodobnosti, která je známá také pod pojmem Gaussova křivka. Tento zvonovitý tvar souvisí s faktem, že variabilita normálního rozdělení kolem jeho střední hodnoty je dána aditivním vlivem mnoha tzv. „slabě působících“ faktorů, což znamená, že se s normálním rozdělením setkáváme u řady biologických a klinických znaků, např. výšky člověka, délky končetin a kostí, maximální dosažené rychlosti ještěrky, apod. Je třeba poznamenat, že označení normální rozdělení neznamená, že by toto rozdělení pravděpodobnosti bylo v přírodě normálnější než rozdělení jiná, na rozdíl od ostatních rozdělení má však normální rozdělení stěžejní význam v teoretické statistice.
Normální rozdělení pravděpodobnosti je zcela popsáno dvěma parametry, které jsou standardně označovány jako µ a σ2, kdy první z nich představuje střední hodnotu normálního rozdělení a druhý představuje rozptyl normálního rozdělení. Fakt, že náhodná veličina X má normální rozdělení pravděpodobnosti se střední hodnotou µ a rozptylem σ2, zapisujeme jako X ~ N(µ,σ2). Hustota náhodné veličiny X pak má následující tvar:
|
|
(4.11) |
Ukázky hustot náhodných veličin s normálním rozdělením pro různé hodnoty parametrů µ a σ2 jsou uvedeny na obrázku 4.1.
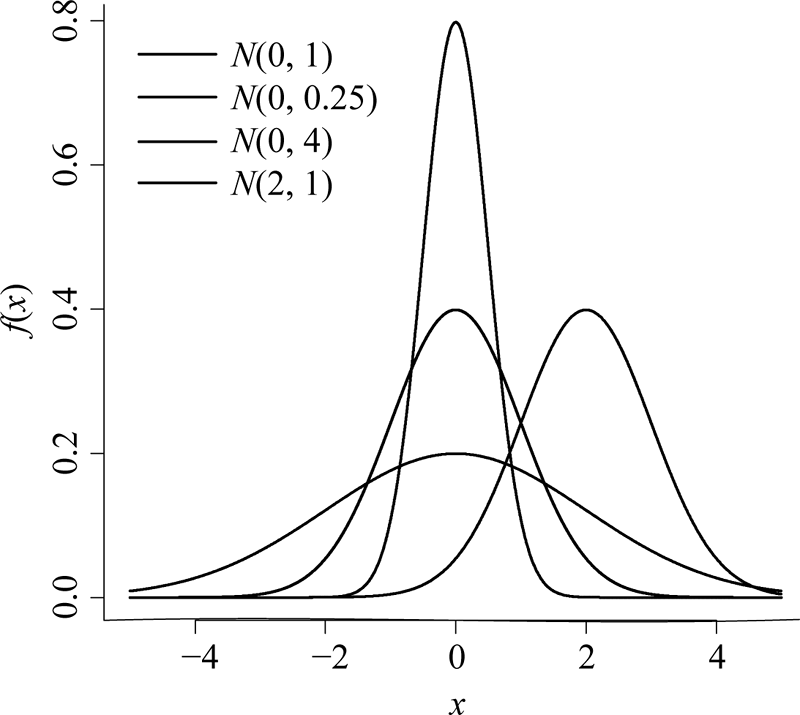
Obr. 4.1: Ukázky hustot náhodných veličin s normálním rozdělením.
Jak již bylo uvedeno, normální rozdělení pravděpodobnosti je pro biostatistiku důležité, neboť je klíčovým předpokladem řady základních testů a modelů. Rozhodneme-li se použít pro zpracování dat metodu založenou na předpokladu, že data pocházejí z normálního rozdělení, je ověření tohoto předpokladu stejně důležité jako výběr samotného testu. Pro ověření normality existuje řada testů a grafických metod, některé z nich budou rozebrány ve výukové jednotce Analýza rozptylu (ANOVA) v části Hodnocení normality pozorovaných hodnot v souvislosti s analýzou rozptylu, což je právě jedna z metod postavených na předpokladu normálního rozdělení. Nicméně stoprocentně ověřit to, zda se sledovaná veličina (znak) chová dle normálního rozdělení je prakticky nemožné, vždy jsme totiž limitováni množstvím a kvalitou pozorovaných dat. V praxi tak normalitu vlastně nepotvrzujeme, spíše připouštíme, že se pozorované hodnoty neodchylují až příliš.
Vlastností normálního rozdělení s velkým praktickým významem je, že jsme u něj schopni vyčíslit procento pozorování, která by se měla realizovat v rozmezí ± x-násobku směrodatné odchylky σ od střední hodnoty μ. Zmíněná procenta pro jedno, dvou a třínásobek směrodatné odchylky uvádí tabulka 4.2.
Tab. 4.2: Pravděpodobnost realizace normální náhodné veličiny v rozmezí ± x-násobku směrodatné odchylky σ od střední hodnoty μ.
| Interval | Pravděpodobnost realizace uvnitř intervalu | Pravděpodobnost realizace vně intervalu |
|
|
0,683 | 0,317 |
|
|
0,954 | 0,046 |
|
|
0,997 | 0,003 |
Z tabulky 4.2 vyplývá, že pravděpodobnost realizace náhodné veličiny s normálním rozdělením v intervalu μ ± 2σ je lehce přes 95%. Jinými slovy, zhruba 95% pozorování náhodné veličiny s normálním rozdělením by se mělo realizovat v rozmezí μ – 2σ a μ + 2σ. Uvážíme-li dokonce interval μ ± 3σ, pak je pravděpodobnost realizace náhodné veličiny uvnitř tohoto intervalu dokonce více než 99,5%. Tato jednoduchá poučka je někdy označována jako pravidlo ± 3 sigma.
Další důležitou vlastností normálního rozdělení, která má praktické využití, je, že při sčítání dvou a více náhodných veličin se zachovává normalita. Jinými slovy, pro nezávislé náhodné veličiny X a Y platí, že i jejich součet, tedy náhodná veličina Z = X + Y, má normální rozdělení pravděpodobnosti.




