Hodnocení normality pozorovaných hodnot

Hodnocení normality pozorovaných hodnot je klíčovým postupem v biostatistice, neboť náhodný výběr z normálního rozdělení je kromě analýzy rozptylu předpokladem i řady dalších základních testů a modelů. Zamítnutí normality rozdělení pozorovaných hodnot však nemusí znamenat povolení nebo zamítnutí použití příslušného testu, ale může např. indikovat odlehlé a nelogické hodnoty v datovém souboru.

Posouzení, zda pozorované hodnoty pochází z normálního rozdělení pravděpodobnosti, není vůbec jednoduché a statistické testy nemusí být nutně nejlepším nástrojem. Vždy je důležité pozorované hodnoty zobrazit pomocí dostupných grafických nástrojů. Základní nástroje pro hodnocení normality pozorovaných dat jsou následující:

• Q-Q diagram. Tento grafický nástroj umožňuje posoudit, zda pozorované hodnoty pochází z nějakého známého rozdělení pravděpodobnosti. Q-Q diagram proti sobě zobrazuje na ose x kvantily teoretického rozdělení pravděpodobnosti (v našem případě normálního rozdělení) a na ose y kvantily pozorovaných hodnot. V případě shody výběrového rozdělení dat s teoretickým rozdělením leží všechny body na přímce, zatímco neshodují-li se výběrové a teoretické rozdělení, budou zobrazené body vytvářet křivku odlišnou od přímky. Čtyři příklady Q-Q diagramu jsou znázorněny na obrázku 8.1, kde jsou srovnány simulované hodnoty ze čtyř různých rozdělení pravděpodobnosti s kvantily standardizovaného normálního rozdělení N(0,1). Vlevo nahoře vidíme ideální shodu pozorovaných a teoretických kvantilů danou tím, že hodnoty byly simulovány taktéž z rozdělení N(0,1). Vpravo nahoře jsou také zobrazeny hodnoty simulované z rozdělení N(0,1), ke kterým však byly přidány tři odlehlé hodnoty. Výsledkem je graf, kde téměř všechny zobrazené body leží na přímce, výjimkou jsou právě tři odlehlé hodnoty, které lze jednoznačně identifikovat. Vlevo dole jsou v Q-Q diagramu zobrazeny simulované hodnoty z logaritmicko-normálního rozdělení s parametry 0 a 1, výsledná křivka je typická pro srovnání pozorovaných hodnot z asymetrického rozdělení pravděpodobnosti s normálním rozdělením. Vpravo dole pak vidíme Q-Q diagram pro hodnoty pocházející z rovnoměrně spojitého rozdělení na intervalu (0,1).
• Shapirův-Wilkův test byl primárně odvozen pro hodnocení normality u menších výběrových souborů (n mezi 3 a 50), v roce 1982 však byl rozšířen i pro větší soubory (n do 2000). Shapirův-Wilkův test má přímou souvislost s Q-Q diagramem, neboť je založen na statistickém vyjádření toho, jak moc se křivka zobrazená Q-Q diagramem liší od ideální přímky. Jinými slovy, jedná se o proložení seřazených pozorovaných hodnot regresní přímkou vzhledem k očekávaným hodnotám normálního rozdělení. Tento test je důležitým nástrojem právě v situacích, kdy máme k dispozici pouze omezený počet pozorování a na základě vizualizace pomocí Q-Q diagramu nejsme schopni jednoznačně rozhodnout o tom, zda data jsou či nejsou normálně rozdělená.
• Kolmogorovův-Smirnovovův test představuje obecnější nástroj na hodnocení shody výběrového rozdělení s teoretickým rozdělením pravděpodobnosti, který je založen na srovnání výběrové distribuční funkce s teoretickou distribuční funkcí odpovídající danému (v našem případě normálnímu) rozdělení. Kolmogorovův-Smirnovovův test hodnotí maximální vzdálenost mezi těmito dvěma distribučními funkcemi.

V případě, že některý z předpokladů analýzy rozptylu není splněn, máme na výběr ze dvou možností, buď se pokusíme data transformovat (např. logaritmická transformace nám může pomoci s normalizací výběrového rozdělení nebo se stabilizací rozptylu u logaritmicko-normálních dat) nebo pro testování použijeme neparametrický test. Nejpoužívanější neparametrickou alternativou k analýze rozptylu je Kruskalův-Wallisův test, který nevyžaduje předpoklad normality pozorovaných hodnot.

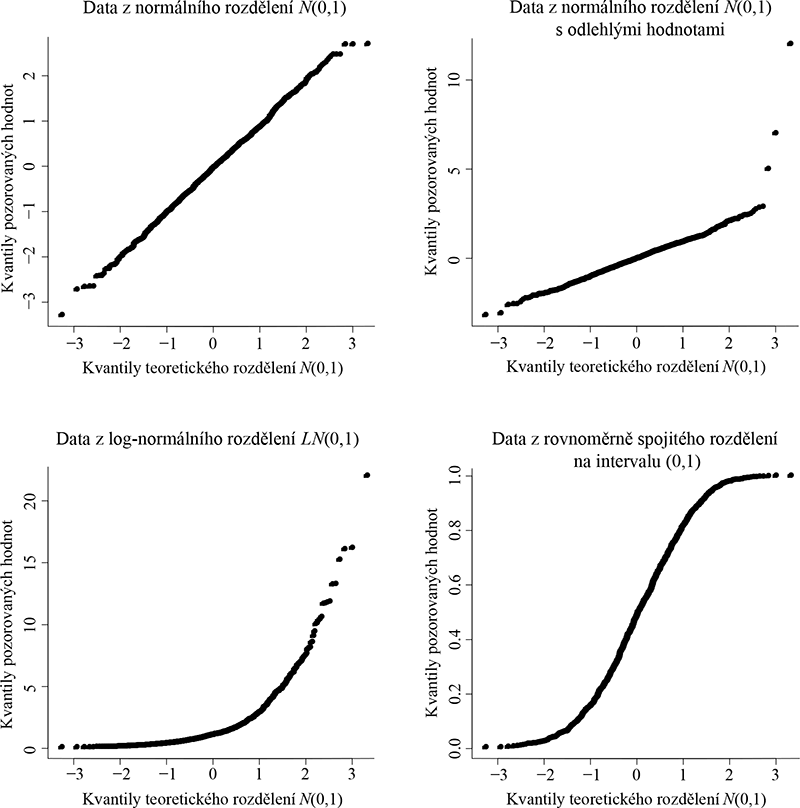
Obr. 8.1: Q-Q diagramy pro srovnání výběrového rozdělení hodnot s rozdělením N(0,1).