Maple provádí přesně numerické výpočty s celými, racionálními i iracionálními čísly. Každý zadaný matematický výraz se snaží co nejvíce zjednodušit (např. zlomek zkrátit a převést na základní tvar, upravit algebraický výraz, ...), ale ne za cenu ztráty přesnosti. To znamená, že například racionální čísla (zlomky) udržuje stále v jejich základním tvaru. Podobně s konstantami π, e a dalšími, s odmocninami a jinými výrazy pracuje jako se symboly. Tímto je zaručena absolutní přesnost výpočtů v Maple i v případě, kdy nepracuje pouze s celými čísly.

Jsou však situace, kdy potřebujeme znát přibližnou hodnotu reálného nebo racionálního čísla v pohyblivé řádové čárce. K tomu slouží příkaz evalf, jenž vrátí zaokrouhlenou hodnotu svého argumentu na počet platných cifer mantisy specifikovaný systémovou proměnnou Digits. Ta je standardně nastavena na hodnotu 10. Všechny výpočty, při nichž je nutné zaokrouhlovat čísla, provádí proto Maple s přesností na 10 platných míst. Proměnnou Digits můžeme nastavit na takřka libovolné přirozené číslo. Omezení, jak vysoké toto číslo může být, zjistíme příkazem kernelopts(maxdigits). Pro představu uveďme, že pro Maple 2015 je toto číslo 38 654 705 646, tedy více než 38 miliard platných cifer, s kterými dokáže systém počítat.

Maple rozeznává přesná čísla (mezi něž patří i zmíněné symboly π a e, zlomky atd.) a čísla typu Floating-Point, nebo-li čísla v pohyblivé řádové čárce (např. -2.76E10, 234.567, ). Jestliže v zápisníku zadáme výraz, v němž některý z jeho podvýrazů bude typu Floating-Point, může Maple na celý výraz pohlížet jako by byl tohoto typu a bude výsledky výpočtů zaokrouhlovat.

K provedení výpočtu v zápisníku máme zpravidla více možností. Jednak pomocí příkazů jazyka Maple, tj. když chceme vypočítat například odmocninu z čísla 2.5, zapíšeme v systému Maple příkaz sqrt(2.5). Stejného výsledku dosáhneme použitím symbolu pro odmocninu z palety Expression, viz obr. 3.17.

Pokud chceme určit nejmenší společný násobek čísel 10, 12 a 15, můžeme využít příkazu Maple lcm, nebo zapsat čísla na řádek za sebe (oddělená čárkami), označit je myší a pomocí jejího pravého tlačítka zvolit z kontextové nabídky funkci Apply Function > Least Common Multiple, viz obr. 3.17, 3.18.

Obrázek 3.17: Různé možnosti provedení výpočtu

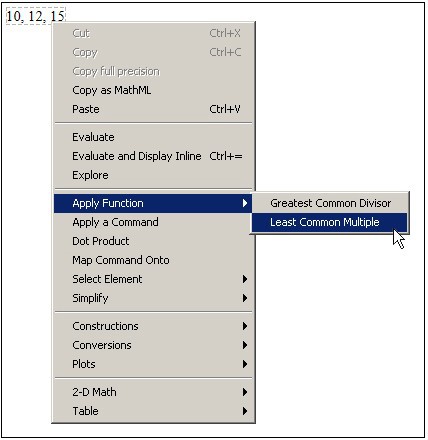
Obrázek 3.18: Provedení výpočtu pomocí kontextové nabídky

Každému zobrazenému výsledku se v zápisníku přiřazuje číselné označení, které se zapisuje zcela vpravo na řádek s odpovídajícím výsledkem. Díky číselnému označení se lze na předešlé výsledky odvolávat a používat je při tvorbě dalších příkazů, viz obr. 3.19. Z důvodu jednoduchosti budeme v dalším číselné označení vynechávat.

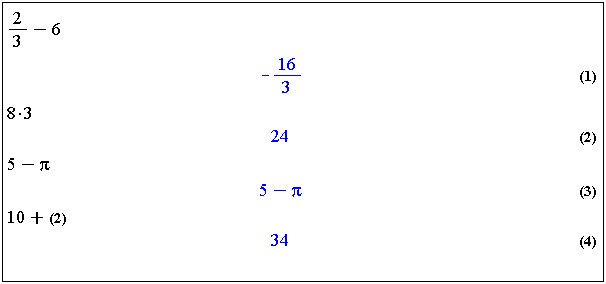
Obrázek 3.19: Označení výsledků

Číselné označení výsledků je možné potlačit (tj. nezobrazovat), znovu vyvolat, případně upravit jeho formát v HLAVNÍM MENU (Format > Equation Labels > ...).

Pokud chceme například přičíst k číslu 10 výsledek s označením (2), viz obr. 3.19, pak napíšeme „10+“ a současným stisknutím kláves „Ctrl a L“ vložíme požadované označení výsledku (tj. do vyskakujícího okna „pop-up“ zadáme číslo 2 a potvrdíme (OK), viz obr. 3.20).

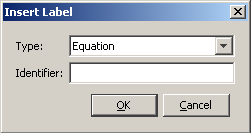
Obrázek 3.20: Vyskakující okno „pop-up“ pro zadání označení výsledku

Místo současného stisku kláves „Ctrl a L“ je možné použít HLAVNÍ MENU (Insert > Label ...).

Pozor však, zapíšeme-li na klávesnici jako číselné označení výsledku text „(2)“ při tvorbě příkazu, tak se výsledek číselně označený (2) na obr. 3.19 do příkazu nepřenese. Pro vložení výsledku z číselného označení do příkazu Maple je třeba důsledně používat předešlý postup s „vyskakujícím okénkem“ zobrazeným na obr. 3.20.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity