Algoritmizace
Ve vývoji matematického modelu je důležitá jeho algoritmizace pro nalezení jeho řešení (s využitím jak numerických metoda, tak ICT, včetně Maple). Existují dva hlavní způsoby algoritmizace matematického modelu vedoucí k nalezení jeho řešení. Rozlišujeme algoritmy pro nalezení:
- Analytického (explicitního) řešení, které spočívá v nalezení přesného řešení modelu pomocí analytických matematických metod (řešení soustav lineárních, nelineárních, algebraických, diferenciálních, integrálních a diferenciálně algebraických rovnic, řešení optimalizačních úloh s volnými a vázanými extrémy apod.) s využitím aplikačních software symbolických výpočtů (Maple, Mathematica apod.).
- Numerického (přibližného) řešení, které se používá při řešení modelů, u kterých neumíme (nebo nechceme) řešit model analyticky, nebo v případech, kdy je analytické řešení příliš složité nebo obtížné a složité (metody Monte Carlo, simulace na počítači apod.). Algoritmus sestavujeme s využitím aplikačních software pro numerické výpočty (Maple, Mathematica, Matlab, R, Octave apod.) s využitím numerických metod [8]. Při numerickém řešení musíme uvažovat jeho numerickou stabilitu, konvergenci přibližného řešení k přesnému řešení a chybu, která nám vznikne při aproximaci přesného řešení. Dále je vhodné uvažovat i fyzikální rozměr výsledného řešení (např. délka, hmotnost objektů by neměla být záporná apod.).
Přepokládejme, že čtenář má již vytvořen samostatný účet s jeho přiděleným jménem a může vyhledat Příklad 3 v systému MapleCloud, kde ukážeme rozdíl mezi analytickým řešením a numerickým řešením matematického modelu systému výskytu sezónní chřipky v Maple.
Příklad 3: Analytické a numerické řešení matematického modelu systému výskytu sezónní chřipky v Maple.
Analytické řešení
Navážeme na příklad 2, kde jsme vyvinuli matematický model a popsali jsme jej soustavou diferenciálních rovnic (1)-(3), kterou jsme uložili v Maple do proměnné odesys, a dále počátečními podmínkami (4), které jsme uložili do proměnné init.
Analytické řešení vypočítá Maple pomocí příkazu dsolve pro soustavu diferenciálních rovnic uloženou v proměnné odesys.
Analytické řešení Infective(t) je kořenem (v Maple to je označováno pomocí RootOf) velmi složité funkcionální rovnice, v níž se vyskytují pomocné proměnné _a (integrační proměnná), a _Z (horní hranice integračního intervalu) v integrálu a neznámé konstanty _C2 a _C3, které jsou závislé na počátečních podmínkách (4). Řešení Suspectible(t) je podílem čitatele, kde je součet násobku řešení Infective(t) a jeho derivace a čitatele, kde je
násobek řešení Infective(t). Řešení Removed(t) je součtem integrálu z
násobku řešení Infective(t) a neznámé konstanty _C1, která je závislá na počátečních podmínkách (4).
Získané analytická řešení Infective(t), Suspectible(t), Removed(t) bychom mohli v Maple dále symbolicky upravovat, ale dostali bychom velmi komplikované výrazy, proto je ponecháme v tomto uzavřeném tvaru.
|
|
Vidíme, že analytické řešení je buď konstantní když počet infikovaných jedinců je nulový nebo je velmi komplikované. Pokud budeme uvažovat obecné počáteční podmínky (4), tak je možné vypočítat analytické řešení opět pomocí příkazu dsolve
avšak získáme ještě komplikovanější výrazy, proto toto analytické řešení je uvedeno pouze v příkladu 3 na MapleCloud a na obr. 9, v dalším příkladu.
Numerické řešení
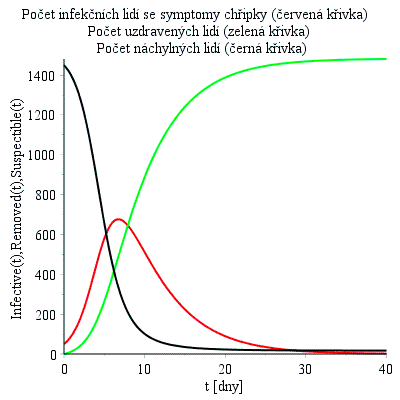
Maple rovněž umožnuje vypočítat přibližné řešení počátečního problému (1) - (4) a zobrazit grafy průběhu řešení Suspectible(t), Infective(t) a Removed(t) v zvoleném intervalu. Nejprve musíme specifikovat parametry a
, počáteční podmínky S0 a I0. Počet jedinců v populaci je N = S0 + I0. Tyto údaje jsme převzali z [5]. Numerické řešení počátečního problému (1) - (4) pomocí příkazu dsolve a výsledné přibližné řešení (proceduru Maple) uložíme do strukturované proměnné res.
Dále využijeme funkci odeplot z balíku plots v Maple, kterou vykreslíme přibližné řešení na intervalu [0, 40] na obr. 2.