Modifikace modelu

Modifikace modelu a jeho vylepšení. V případě, že vypočtené řešení není v dostatečném souladu se zkoumaným systémem (objektivní realitou), je nutno v procesu matematického modelování s využitím ICT začít znovu postupovat od kroku identifikace modelu a opakovat celý předešlý postup matematického modelování do té doby, dokud nedosáhneme uspokojivého řešení zkoumaného problému, viz obr. 1. Metody prezentace modelu, pomocí jeho implementovaného aplikačního programu a vypočteného řešení jeho potenciálním uživatelům závisí na jejich znalostech zkoumaného systému a matematického modelování obecně. Pokud uživatel nechce vědět o detailech implementace modelu, je vhodné ukázat mu všechny relevantní informace o výstupech řešení modelu systému. To umožní uživateli (který není matematickým modelářem nebo programátorem) vytvořit si objektivnější pohled na řešení modelu systému a jeho interpretaci. Je vhodné zkontrolovat, zda získané řešení u dynamických úloh umožňuje i jeho extrapolace v čase. Tyto extrapolace mohou usnadnit pochopení řešení modelu systému buď vzhledem k použitým datům při vytváření modelu, nebo vzhledem k datům použitým při testování modelu.

Příklad 6: Modifikace modelu výskytu sezónní chřipky

V předchozích příkladech jsme vytvořili a analyzovali model pro předpovídání kulminace výskytu chřipky u obyvatel daného regionu. Ukázalo se, že tento model bude třeba zpřesnit. Nyní vytvoříme zpřesněný model, v němž rozdělíme populaci N obyvatel do více skupin. Označíme opět Suspectible(t) počet jedinců v čase v skupině náchylných lidí, tj. zdravých lidí, kteří nemají proti chřipce imunitu a mohou jí onemocnět. Počet jedinců v čase ve skupině infekčních lidí Infective(t) z předchozích příkladů rozdělíme na skupinu Infective1(t) infekčních jedinců se symptomy nemoci a skupinu Infective2(t) infekčních jedinců bez symptomů nemoci. Dále označme Removed(t) počet jedinců v čase ve skupině uzdravených lidí, tj. těch, kteří nemoc již prodělali a jsou proti nemoci nadále imunní a Vaccinated(t) počet jedinců v čase t ve skupině očkovaných lidí, tj. lidí, kteří nemoc neprodělali, ale díky očkování jsou vůči ní imunní a Dead(t) počet jedinců v čase t ve skupině zesnulých lidí, tj. těch, kteří nemoci podlehli. Součet všech jedinců v čase z předchozích skupin dá celkový počet N lidí. Budeme přepokládat, že:

• jedinec může během sledovaného období (listopad až duben) onemocnět chřipkou nejvýše jednou;
• očkovaný jedinec ze skupiny Vaccinated(t) je během sledovaného období plně imunní (nemůže onemocnět chřipkou);
• všichni jedinci z libovolné (ale pevně zvolené) skupiny jsou si rovni (tj. např. nehledě na jejich věk či zdravotní stav)
• N, tj. počet jedinců ve zkoumaném regionu, je během sledovaného období konstantní, tj. platí pro pro libovolné :
•                        

  (5)

• přechod člověka z jedné skupiny do jiné závisí pouze na konstantním parametru a velikosti skupiny, z níž přechází, s výjimkou přechodu ze skupiny náchylných lidí do skupiny infekčních lidí bez symptomů nemoci, který je tím častější, čím více je infekčních lidí.

Na základě zmíněných předpokladů sestavíme nový modifikovaný model [7]. Čas t budeme přitom chápat jako spojitou veličinu. Parametry  a vystupující v modifikovaném modelu jsou nezáporná reálná čísla nejvýše rovná jedné (tj. z příslušné skupiny se nemůže přesunout do jiné skupiny více lidí, než kolik jich tam je). Tento model tvoří soustava lineárních diferenciálních rovnic 1. řádu [7]:

	(6)
	(7)
	(8)
	(9)
	(10)
	(11)

s obecnými počátečními podmínkami pro :

(12)

přičemž platí .

Model (5)-(12) budeme řešit pomocí Maple podobně jako v příkladu 5 s využitím komponet Slider pro zadávání a změny hodnot parametrů a v rovnicích (6) – (11), dále komponet MathContainer pojmenovaných SMathContainer, I1MathContainer, I2MathContainer, RMathContainer, VMathContainer a DMathContainer, pro interaktivní zadávání počátečních podmínek (12). Komponenty Label sdružené s komponentami MathContainer budou využity k zobrazení hodnot parametrů. Komponenty Plot zobrazí interaktivní grafy numerického řešení modifikovaného modelu (6) – (12)). Takto vytvořený zápisník, viz obr. 11, uložíme do systému MapleCloud jako příklad 6, kde jej budou moci využívat všichni uživatelé ve skupině public. Program sdružený s komponentou Buton pojmenovanou Aktualizuj podmínky, který načte počáteční hodnoty (12) pomocí komponent MathContainer, spočítá numerické řešení modelu (6) – (12) a zobrazí jeho grafy (obr. 11) pomocí komponent Plot pojmenových Plot01 a Plot02 má tvar:

use DocumentTools in
S0:=Do(%SMathContainer); #vstup hodnoty S0 ze zadávacího okna
I1:=Do(%I1MathContainer); #vstup hodnoty I1 ze zadávacího okna
I2:=Do(%I2MathContainer); #vstup hodnoty I2 ze zadávacího okna
V0:=Do(%VMathContainer); #vstup hodnoty V0 ze zadávacího okna
R0:=Do(%RMathContainer); #vstup hodnoty R0 ze zadávacího okna
D0:=Do(%DMathContainer); #vstup hodnoty D0 ze zadávacího okna
N:=S0 + I1 + I2 + V0 + R0 + D0;
init:=Suspectible(0)=S0, Infective1(0)=I1, Infective2(0)=I2, Removed(0)=R0, Vaccinated(0)=V0, Dead(0)=D0;
odesys := diff(Suspectible(t),t) = -beta*Suspectible(t)*(Infective1(t)+Infective2(t))/N-mu*Suspectible(t),
diff(Infective1(t),t) = alpha*Infective2(t)-(ny+delta)*Infective1(t),
diff(Infective2(t),t) = beta*Suspectible(t)*(Infective1(t)+Infective2(t))/N-(alpha+kappa+mu)*Infective2(t),
diff(Removed(t),t) = ny*Infective1(t)+kappa*Infective2(t),
diff(Vaccinated(t),t) = mu*(Suspectible(t)+Infective2(t)),
diff(Dead(t),t) = delta*Infective1(t);
res := dsolve([odesys,init], numeric);
Do(%Plot01=plots[odeplot](res,[[t,Removed(t)],[t,Infective1(t)]],0..90, labels=["t [dny]", "Removed(t), Infective1(t)"],labeldirections=[horizontal,vertical],title="Počet uzdravených lidí (zelená křivka)n Počet infekčních lidí se symptomy chřipky (červená křivka)",thickness=2, color=[green,red]));
Do(%Plot02=plots[odeplot](res,[[t,Infective2(t)],[t,Vaccinated(t)],[t,Dead(t)]],0..90, labels=["t [dny]","Infective2(t), Vaccinated(t), Dead(t)"],title="Počet infekčních lidí bez symptomů chřipky (modrá křivka)n Počet očkovaných lidí (hnědá křivka)n Počet zesnulých lidí (černá křivka)",thickness=2, color=[blue,brown,black]));
end use;

Programy sdružené s komponentami Slider, které budou načítat hodnoty parametrů a v rovnicích (6) – (11) jsou podobné a uvedeme pouze program pro slider pro parametr α pojmenovaný alphaSlider má tvar:

use DocumentTools in
Do(alpha=%alphaSlider(value));
Do(%alphaLabel(caption)=%alphaSlider(value));
S0:=Do(%SMathContainer); #vstup hodnoty S0 ze zadávacího okna
I1:=Do(%I1MathContainer); #vstup hodnoty I1 ze zadávacího okna
I2:=Do(%I2MathContainer); #vstup hodnoty I2 ze zadávacího okna
V0:=Do(%VMathContainer); #vstup hodnoty V0 ze zadávacího okna
R0:=Do(%RMathContainer); #vstup hodnoty R0 ze zadávacího okna
D0:=Do(%DMathContainer); #vstup hodnoty D0 ze zadávacího okna
N:=S0 + I1 + I2 + V0 + R0 + D0;
init:=Suspectible(0)=S0, Infective1(0)=I1, Infective2(0)=I2, Removed(0)=R0, Vaccinated(0)=V0, Dead(0)=D0;odesys := diff(Suspectible(t),t) = -beta*Suspectible(t)*(Infective1(t)+Infective2(t))/N-mu*Suspectible(t),
diff(Infective1(t),t) = alpha*Infective2(t)-(ny+delta)*Infective1(t),
diff(Infective2(t),t) = beta*Suspectible(t)*(Infective1(t)+Infective2(t))/N-(alpha+kappa+mu)*Infective2(t),
diff(Removed(t),t) = ny*Infective1(t)+kappa*Infective2(t),
diff(Vaccinated(t),t) = mu*(Suspectible(t)+Infective2(t)),
diff(Dead(t),t) = delta*Infective1(t);
res := dsolve([odesys,init], numeric);
Do(%Plot01=plots[odeplot](res,[[t,Removed(t)],[t,Infective1(t)]],0..90, labels=["t [dny]", "Removed(t), Infective1(t)"],labeldirections=[horizontal,vertical],title="Počet uzdravených lidí (zelená křivka)n Počet infekčních lidí se symptomy chřipky (červená křivka)",thickness=2, color=[green,red]));
Do(%Plot02=plots[odeplot](res,[[t,Infective2(t)],[t,Vaccinated(t)],[t,Dead(t)]],0..90, labels=["t [dny]","Infective2(t), Vaccinated(t), Dead(t)"],labeldirections=[horizontal,vertical], title="Počet infekčních lidí bez symptomů chřipky (modrá křivka)n Počet očkovaných lidí (hnědá křivka)n Počet zesnulých lidí (černá křivka)",thickness=2, color=[blue,brown,black]));
end use;

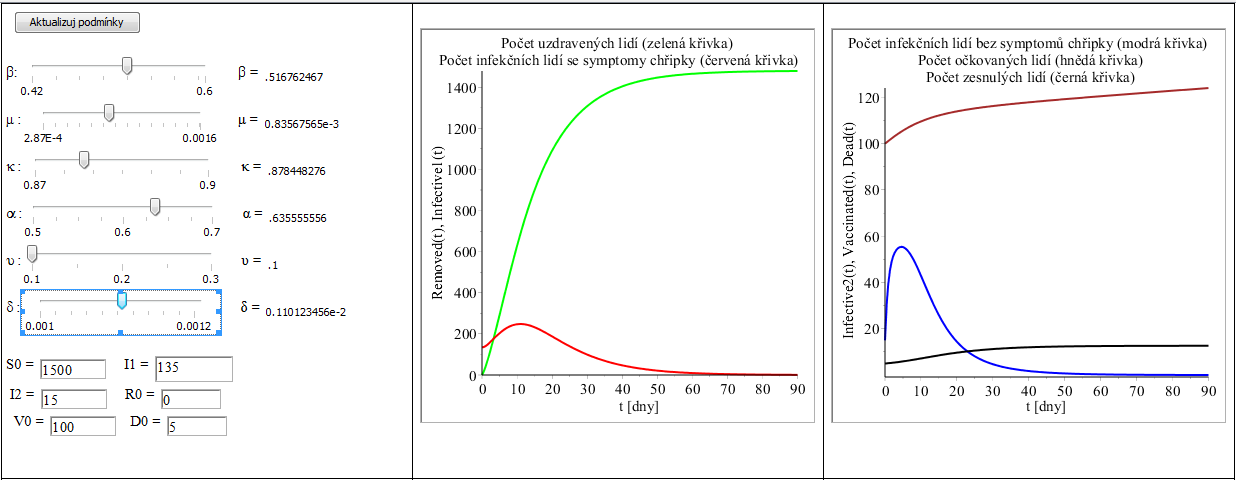
Obr. 11. Numerické řešení mofikovaného modelu (5)-(12 pro zvolené hodnoty parametrů a , které je možno interaktivně měnit na posuvnících a počátečními podmínkami Suspectible(0)=1500, Infective1(0)=135, Infective2(0)=15, Removed(0)=0, Vaccinated(0)=100, Dead(0)=5 a grafy řešení Removed(t), Infective1(t), Infective2(t), Vaccinated(t) a Dead(t)