Metoda prohledávání do hloubky, Depth-first search (DFS)

Popis

Metoda patří spolu s BFS mezi základní prohledávací algoritmy. Algoritmus DFS prohledává strom uzlů tak, že se nejlevější větví stromu postupně zanořuje do maximální možné hloubky, tedy do konce této větve, nebo do nalezení cíle. Poté se vrací o jeden krok zpět a provádí analogicky zanoření pro další větev aktuálně zpracovávaného uzlu. Neprochází tedy strom postupně po jednotlivých úrovních jako BFS, ale rekurzivně po jednotlivých podstromech daného uzlu. Zjednodušeně lze chápat tuto prohledávací metodu jako rekurzivní volání funkce „Vyhodnoť“ – vyhodnoť, zda je zpracovávaný uzel cílem a když není, vyhodnoť tuto podmínku pro jeho následníka zleva.

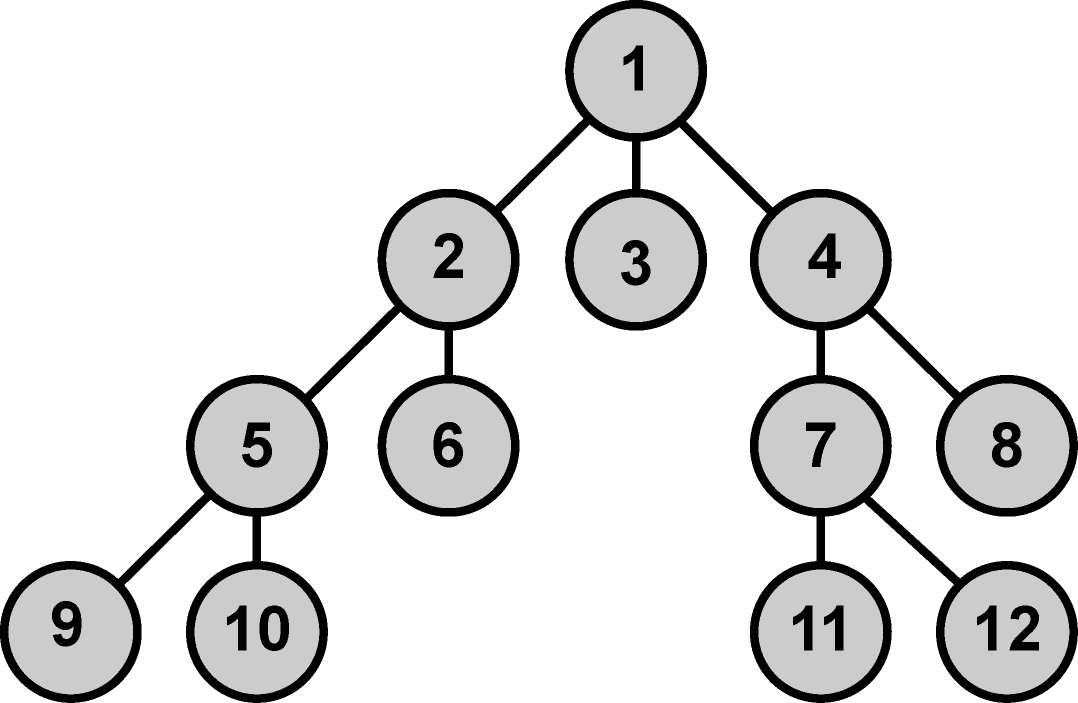
Obr. 7. Prohledávací strom - příklad.

Začátek generování cesty algoritmu DFS lze pro předcházející graf zkráceně demonstrovat následujícím zápisem:

[(1)]  -> [(2,1) (3,1) (4,1)]  -> [(5,2,1) (6,2,1) (3,1) (4,1)] -> [(9,5,2,1)(10,5,2,1) (6,2,1) (3,1) (4,1)] -> [(10,5,2,1) (6,2,1) (3,1) (4,1)] -> [(6,2,1) (3,1) (4,1)] -> [(3,1) (4,1)] -> [(4,1)] -> [(7,4,1) (8,4,1)] …

Podoba množin OPEN a CLOSE procházených stavů bude pro tuto sekvenci následující:

OPEN[1], CLOSE[] ->OPEN[2, 3, 4], CLOSE[1]   -> OPEN[5, 6, 3, 4], CLOSE[1, 2]  ->OPEN[9, 10, 6, 3, 4], CLOSE[1, 2, 5] ->OPEN[10, 6, 3, 4], CLOSE[1, 2, 5, 9] ->OPEN[6, 3, 4], CLOSE[1,2,5,9,10] -> OPEN[3,4], CLOSE[1, 2, 5,9, 10, 6]  ->OPEN[4], CLOSE[1, 2, 5,9, 10, 6, 3] ->OPEN[7, 8], CLOSE[1, 2, 5,9, 10, 6, 3, 4] …

Generování této cesty odpovídá principu datové struktury zásobníku LIFO (last in, first out), kdy je vždy vybrán první, nejlevější uzel z množiny (zásobníku) OPEN, ten je prověřen a v případě, že nepatří mezí cílové stavy, je expandován. Nově vygenerované uzly jsou zařazeny na začátek množiny, vrchol zásobníku. Algoritmus pracuje tak dlouho, dokud nenarazí na první cílový stav, nebo dokud nevyčerpá celý stavový prostor – množina OPEN je prázdná.

Algoritmus:

1. Inicializuj množiny OPEN=[], CLOSE=[].
2. Vlož počáteční stav do OPEN.
3. Pokud je množina OPEN prázdná, ukonči algoritmus, řešení neexistuje. Jinak pokračuj dalším bodem.
4. Vyjmi první stav zleva z množiny OPEN a prověř, zda se nejedná o cílový stav. Pokud ano, máme řešení a algoritmus končí. V opačném případě vyjmutý stav drž v paměti a pokračuj dalším bodem.
5. Zapiš vyjmutý stav do CLOSE.
6. Prověř, expanduj vyjmutý stav generuj jeho následníky, další stavy.
7. Vlož všechny následníky stavu kteří nejsou v množině CLOSE na začátek množiny OPEN.
8. Pokračuj bodem 3.

Vlastnosti algoritmu

Pro obecně definovaný strom není algoritmus úplný, neboť může uváznout v nekonečně dlouhé větvi, nicméně v případě konečné délky větví jej lze považovat za úplný.  Algoritmus není optimální, nalezené řešení nemusí být řešením ležícím v minimální hloubce, tedy řešením s minimální délkou cesty z počátečního uzlu.

Časová složitost algoritmu je stejně jako pro BFS exponenciální, kdy počet navštívených uzlů odpovídá maximální hloubce zanoření m a pro faktor větvení ji můžeme vyjádřit jako

(6)

Prostorová složitost je lineární. Minimálně je zapotřebí udržovat v paměti množinu OPEN, která obsahuje jen aktuálně prohledávanou větev, kterou se algoritmus v případě nenalezení cíle v této větvi rekurzivně vrací.

(7)

Výhody a nevýhody

Hlavní výhodou je dobrá prostorová složitost, která odpovídá nejdelší větvi v grafu a tedy relativně malé nároky na paměť počítače při implementaci algoritmu. Nevýhodou je naopak, že metoda není pro nekonečné obecné stromy úplná. Tuto limitaci lze ale relativně snadno potlačit modifikací metody, jak si ukážeme dále. Metoda také není optimální, což může být v případě úloh, kdy hledáme pouze nejlepší možné řešení důvodem pro nepoužití této metody.

Časová složitost je opět jen průměrná. K časové i prostorové složitosti je ale třeba poznamenat a uvědomit si, že v případě řešení reálné úlohy může být hloubka d nalezeného cíle mnohem menší než maximální hloubka m a algoritmus tak není nucený ve všech případech nejdelší větev skutečně expandovat.