Klasifikační možnosti vícevrstvého perceptronu - Kolmogorova věta

Při vyjádření klasifikačních schopností a výpočetní síly vícevrstvých perceptronů můžeme vyjít z  Kolmogorovy věty, která říká:

„Každou vícerozměrnou reálnou spojitou funkci -proměnných lze přesně vyjádřit jako lineární kombinaci konečného počtu spojitých nelineárních funkcí jedné proměnné.“

(4)

kde jsou nelineární funkce jedné proměnné.

Pokud budeme uvedenou větu vnímat v oblasti realizace umělých neuronových sítí a budeme hledat analogii, zjistíme, že vícevrstvý perceptron poskytuje pro realizaci uvedené věty dostatek prostředků. Jednotlivé nelineární funkce požadované Kolmogorovou větou mohou být realizovány pomocí nelineárních, například sigmoidálních funkcí jednotlivých neuronů. Lineární kombinace a tedy sumační vztahy Kolmogorovy věty pak odpovídají výpočtu aktivační funkce jednotlivých neuronů skrytých vrstev.

Uvedený vztah tedy vlastně odpovídá výpočtu, který realizuje vícevrstvý perceptron s  vstupními neurony, neurony první skryté vrstvy s funkcemi neurony druhé skryté vrstvy s funkcemi a jedním neuronem výstupním. Podmínkou je použití neuronů se spojitými, monotónně rostoucími aktivačními funkcemi ve skrytých vrstvách.

Kolmogorovu větu lze formulovat ještě obecněji, dle [1].

(5)

kde tedy došlo ke zmírnění požadavků na obecně různé aktivační přenosové funkce neuronů v jednotlivých vrstvách a nahrazení obecně různých funkcí v různých vrstvách pouze funkcí a jejím násobením koeficientem

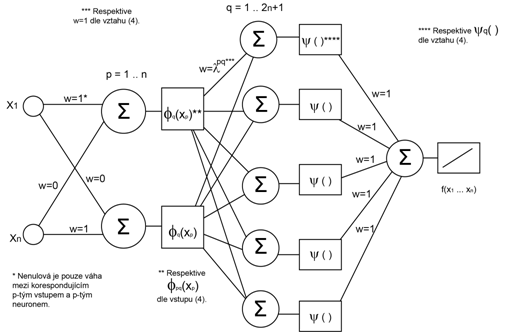
Obr. 14. Kolmogorova věta pro vícevrstvý perceptron

Poněkud problematická může být dle [1] volba funkcí a neboť pro přesnou aproximaci funkce mohou mít tyto hledané funkce vlastnosti, které neumožňují jejich použití jako přechodové výstupní funkce neuronu, protože funkce nejsou obecně hladké.

I přes relativizaci platnosti výše uvedeného závěru Kolmogorovy věty pro vícevrstvý perceptron (nepoužitelnost obecných funkcí jako přenosových funkcí neuronu), bylo dokázáno [3],  že zmnožením počtu neuronů ve skrytých vrstvách je možné dosáhnut univerzální aproximační schopnosti vícevrstvého perceptronu, pokud se spokojíme pouze s libovolně přesnou aproximací funkce nikoli jejím naprosto přesným vyjádřením.

Důsledek Kolmogorovy věty pro vícevrstvý perceptron můžeme shrnout tak, že vícevrstvý perceptron se dvěma skrytými vrstvami, dostatečným počtem neuronů se spojitými monotónně rostoucími aktivačními funkcemi může být univerzálním aproximátorem libovolné funkce N proměnných. To představuje značnou výpočetní sílu.  Dokonce tak velkou, že pro řadu reálných problémů při jejich přibližném řešení vystačíme s klasifikací do lineárně separabilních množin.

V případě perceptronu dvouvrstvého, tedy perceptronu s jednou skrytou vrstvou, pak můžeme vyjít z výsledků Hornika a Leshna, publikovaných v [1].

Z jejich závěrů plyne, že vícevrstvý perceptron s jednou skrytou vrstvou, dostatečným počtem neuronů (zdá se ) a nepolynomiálními (sigmoidálními) aktivačními funkcemi neuronů skryté vrstvy je univerzálním aproximátorem libovolné funkce proměnných.