Algoritmus zpětného šíření chyby (BP algoritmus)

Algoritmus zpětného šíření chyby je základním algoritmem pro učení vícevrstvých perceptronů. V následujících odstavcích si jej odvodíme. Vektory budeme značit čárkou nad daným symbolem, například

Učením sítě můžeme rozumět optimalizační proces, kdy síť nastavuje své parametry tak, aby minimalizovala chybovou funkci vznikající jako rozdíl mezi skutečným a požadovaným výstupem. Pro jeden vstupní vektor platí, že síť realizuje zobrazení

(8)

Chybový vektor získaný po předložení -tého vektoru trénovací množiny lze zapsat jako

(9)

Okamžitá kvadratická odchylka klasifikace sítě pro -tý vektor trénovací množiny je

(10)

Uvedená kvadratická odchylka je však pouze odchylkou vypočtenou na základě předložení jediného vstupu. Optimální by samozřejmě bylo, kdybychom byli schopni vyjádřit střední kvadratickou odchylku přes všechny možné vstupy sítě. Tyto vstupy však nemáme k dispozici, k dispozici máme pouze trénovací množinu obsahující trénovacích dvojic. Pak můžeme střední kvadratickou odchylku přes všechny vstupy obsažené v trénovací množině vyjádřit jako

(11)

Minimalizací této funkce například gradientní metodou nejstrmějšího sestupu bychom dosáhli nejlepší možné klasifikace sítě ve smyslu střední kvadratické odchylky přes celou trénovací množinu. Střední kvadratická odchylka je evidentně funkcí vah sítě. Jejich změnou je tedy realizován postup k minimalizaci střední kvadratické odchylky. Pro změnu vah neuronu můžeme psát

(12)

kde označuje krok učení a je konstanta určující rychlost adaptace.

Gradient můžeme rozepsat jako

(13)

Výpočet tohoto gradientu je však v praxi vzhledem k velkému počtu prvků v trénovací množině a velkému počtu vah sítě bohužel velmi obtížný i pro nepříliš rozsáhlé sítě. Proto jej nahrazuje výpočtem posloupnosti dílčích gradientů, kdy každý dílčí gradient získaný v jednom kroku učení sítě aproximuje hodnotu gradientu přes celou trénovací množinu.

(14)

Uvědomme si nyní, že výstupní vrstva perceptronu se skládá se samostatných neuronů, kde každý z nich přispívá k celkové chybě perceptronu. Uvažujme nyní jeden samostatný neuron výstupní vrstvy.

Hodnotu gradientu pro výstupní, -tou  vrstvu sítě můžeme pro -tou váhu - tého neuronu této vrstvy vyjádřit dle pravidla o složené derivaci

(15)

Pokud vzorec rozebereme po jednotlivých částech, pak třetí část pravé strany vzorce představuje derivaci vnitřního potenciálu -tého neuronu podle -té váhy. Vnitřní potenciál -tého neuronu je vyjádřen sumou vstupních hodnot násobených vahami Vstupní hodnoty neuronu jsou ale v tomto případě představovány výstupy   z předchozí () té vrstvy, pro výsledek derivace tedy můžeme psát

(16)

Střední část pravé strany vzorce představuje derivaci aktivační výstupní funkce podle vnitřního potenciálu neuronu. Konkrétní parametry aktivační přenosové funkce nemáme v tuto chvíli definovanou, ponechme tedy vztah bez úprav, jen s přepsáním derivace

(17)

Úvodní část vzorce Neuronové sítě - Perceptrony (16) vyjadřující derivaci chyby podle výstupu neuronu můžeme po zvážení výrazů Neuronové sítě - Perceptrony (9) a Neuronové sítě - Perceptrony (10) psát také jako

(18)

Po úpravě tedy dostáváme vztah

(19)

Dosazením do vztahu Neuronové sítě - Perceptrony (12) a vektorovým vyjádřením dostáváme pro úpravu vah jednoho neuronu poslední vrstvy

(20)

Ve vztahu zbývá určit hodnotu chyby  a případně derivaci Chyba je pro neurony výstupní vrstvy zřejmá již ze vtahu Neuronové sítě - Perceptrony (9) a je rovna

(21)

Derivace samozřejmě závisí na konkrétní aktivační výstupní funkci neuron. Oblíbené jsou sigmoidální aktivační funkce, které jsou hladké a monotónní a navíc mají jednoduché vyjádření derivace.

		(22)
		(23)

Abychom omezili vznik lokálních minim chybové funkce, je vhodné volit monotónní funkce. Jako aktivační přenosové funkce ale mohou být ale použity libovolné diferencovatelné funkce.

V tuto chvíli je tedy schopni určit chybu a provést adaptaci neuronů výstupní vrstvy formálně odvozeným vztahem.

Podobně, jako jsme odvodili vzorce pro vrstvu výstupní, můžeme postupovat i v případě neuronů skrytých -tých vrstev, tedy

(24)

kde

(25)

Z uvedených vztahů Neuronové sítě - Perceptrony (18), Neuronové sítě - Perceptrony (24) je zřejmé, že výpočet gradientu chybové funkce pro skryté neurony se od definice pro neurony výstupní vrstvy liší pouze částí definice pro výpočet chyby na výstupu neuronu.

Úpravu vah pro libovolný neuron sítě můžeme tedy vyjádřit jako

(26)

kde pro neurony výstupní vrstvy platí

(27)

A pro neurony vnitřních skrytých vrstev platí

(28)

Uvedené odvozené výrazy Neuronové sítě - Perceptrony (26), Neuronové sítě - Perceptrony (27), Neuronové sítě - Perceptrony (28) se velmi často upravují na vyjádření ve formě

	(29)
	(30)
	(31)

Souvislost s heuristicky odvozeným -pravidlem  pro jeden neuron je zde přímočará.

Pokud si všimneme vzorce Neuronové sítě - Perceptrony (31), je zřejmé, že chyba  na výstupu -tého neuronu -té skryté vrstvy je získána jako součet chyb  všech neuronů na výstupech následující, () vrstvy, kde tato chyba  je násobena derivací přenosové výstupní funkce  a dále hodnotou váhy synapse mezi neurony obou vrstev.

Princip algoritmu zpětného šíření chyby tedy spočívá v určení chyby na výstupech všech neuronů výstupní vrstvy, tu určíme lehce dle vztahu Neuronové sítě - Perceptrony (30). Následně je tato chyba použita i k adaptaci skryté vrstvy a to tak, že se chyba z výstupní vrstvy se vlastně šíří strukturou sítě zpět od výstupní vrstvy na vrstvu předcházející, kde je chyba na výstupu modifikována derivací přenosové funkce neuronu výstupní vrstvy a následně ještě vahou, která k neuronu výstupní vrstvy vede z neuronu vrstvy předcházející. Každému neuronu skryté vrstvy je tedy dopravena chyba, která odpovídá jeho příspěvku k celkové  chybě na výstupní vrstvě. Takto je chyba postupně šířena zpět strukturou sítě od výstupu na všechny vrstvy předcházející. Proto je algoritmus nazýván algoritmem zpětného šíření chyby.

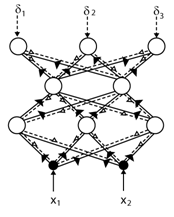Obr. 15. Ilustrace algoritmu zpětného šíření chyby

V bodech lze algoritmus zpětného šíření chyby pro vytvořený vícevrstvý perceptron shrnout jako:

1. Inicializuj váhy sítě.
2. Vyber -tý vzor z trénovací množiny.
3. Předlož ténovací vzor  síti.
4. Urči odezvu sítě  na
5. Urči chybu na výstupu sítě dle Neuronové sítě - Perceptrony (30).
6. Urči chybu na předcházejících vrstvách pomocí zpětného šíření chyby na vrstvy předchozí.
7. Lokálně uprav váhy dle Neuronové sítě - Perceptrony (29).
8. Opakuj od bodu 2, dokud není funkce sítě dostatečně přesná.