Fuzzy množiny
V reálném světě se často snažíme vyjádřit příslušnost daného objektu k nějaké třídě. Uvažujme například člověka. Často použijeme výraz, že tento člověk je například velmi malý, velký, vysoký nebo velmi tlustý. Určitě může být člověk malý a současně spíše tlustý, tedy patřit do více tříd s různou třídou příslušnosti. Nedefinujeme přesně, kolik centimetrů představuje výraz malý, kolik kilogramů tlustý.
Fuzzy množiny řeší přiřazení objektu do dané třídy tzv. mírou (funkcí) příslušností
do té které množiny
(například tlustých lidí), obvykle v intervalu
Fuzzy množina je tedy v univerzu
rovna množině dvojic
|
|
(13) |
Nad fuzzy množinami a
jsou definovány operace, které s nimi umožňují pracovat. Mezi základní patří
| Doplněk | |
| Sjednocení | |
| Odvážné sjednocení | |
| Průnik | |
| Odvážný průnik | |
| Koncentrace | |
| Delatace |
Tab. 2. Operace nad fuzzy množinami
Operace slouží k vytváření nových fuzzy množin. Je tedy možné získat například novou fuzzy množinu malých tlustých lidí tak, že vypočteme průnik těchto množin. Použití operátorů koncentrace a dilatace na fuzzy množinu vysokých lidí lze zase chápat jako vytváření množiny skutečně vysokých lidí (con), případně lidí spíše vysokých (dil).
Fuzzy logika nám tedy pomocí operací a fuzzy množin umožňuje deklarovat pravidla mlhavě.
Opět zopakujme pravidlo platné v produkčních ES systémech Expertní systémy (1), tedy
Jak předpoklady 
tak závěry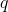 
můžeme modelovat jako fuzzy množiny. Předpokládejme, že nastal nějaký jev, který jsme pozorovali a vložili konkrétní hodnotu popisující tento jev do ES jako nový fakt. Tento fakt může patřit do několika předpokladů 
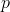a to vždy s různou mírou příslušnosti k danému faktu. Tedy i platnost různých závěrů 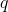je mlhavá, definovaná různou mírou příslušnosti k dané hypotéze. Tedy v případě, že máme například teplotu zvýšenou na 38 °C, ES nám může poradit užít paralen s vysokou mírou příslušnosti, ale stejně tak nám může doporučit, snad s nižší mírou příslušnosti, odcestovat na severní pól.
V konečné fázi rozhodování tak expertní systém využívající fuzzy logiku dospěje do fáze, kdy musí provést defuzzifikaci, tedy převod mlhavých závěrů na konkrétní akci. Může se jednat o výběr jedné nejpravděpodobnější hypotézy (např. dle maxima míry příslušnosti). Může se také jednat o odvození konkrétní hodnoty z nejasných závěrů, kdy například po zvážení všech odlišných faktů dospěje autopilot letadla k závěrům, že má současně spíše (konkrétně dáno funkcí příslušnosti) ubrat plyn, nejlépe ponechat plyn beze změnya současně i plyn velmi silně přidat. Výsledkem ale musí být jedna hodnota, tedy například změň plyn o daný počet procent.V tomto případě je možné postupovat například pomocí výpočtu těžiště plochy pod funkcemi příslušností splněných závěrů. Zde by tedy výsledkem defuzzifikace bylo pravděpodobně částečné přidání plynu, například o 10%.
