Vlastnosti binárních relací na množině

Binární relace na množině mají speciální význam, neboť umožňují zkoumat vlastnosti vztahů mezi prvky patřícími do téže množiny. U relací na množině tedy rozlišujeme vlastnosti, jejichž znalost je pro další studium nutná. Nechť je množina a  je relace na této množině.

Reflexivita: Relace ρ se nazývá reflexivní, jestliže tedy jestliže každý prvek množiny A je v relaci sám se sebou. Příkladem reflexivní relace je identita, relace "být menší nebo rovno", relace dělitelnosti, atd. Také platí, že sjednocení a průnik reflexivních relací je opět reflexivní relace. Složením dvou reflexivních relací vznikne opět reflexivní relace. Inverzní relací k reflexivní relaci je reflexivní relace.

Symetrická relace: Relace ρ se nazývá symetrická, jestliže tedy jestliže každá dvojice prvků, která je spolu v relaci, je spolu v relaci i v opačném pořadí. Příkladem symetrické relace je identita, nerovnost nebo vlastnost typu "mít stejné znaménko". Platí, že sjednocení a průnik symetrických relací je opět symetrická relace. Inverzní relací k symetrické relaci je táž relace (pro symetrickou relaci platí, že ρ^-1 = ρ). Složením symetrických relací vznikne opět symetrická relace.

Antisymetrická relace: Relace ρ se nazývá antisymetrická, jestliže tedy pokud je daná dvojice prvků v relaci nezávisle na jejich pořadí, pak to nutně musí znamenat, že se jedná o tentýž prvek. Příkladem antisymetrické relace je relace "být menší nebo rovno". Je zřejmé, že pokud a ≤ b a zároveň b ≤ a, pak nutně a = b.

Tranzitivní relace: Relace ρ se nazývá tranzitivní, jestliže tedy pokud je prvek x v relaci s prvkem y a prvek y je v relaci s prvkem z, je v relaci i prvek x s prvkem z. Příkladem tranzitivní relace je opět relace "být menší nebo rovno", identita, či relace "být příbuzný" na množině lidí.

Úplná relace: Relace ρ se nazývá úplná, jestliže tedy pokud pro každou dvojici prvků platí, že je buď jeden v relaci s druhým, nebo druhý v relaci s prvním. Příkladem úplné relace je například relace ≤ na libovolné číselné množině. Je zřejmé, že pro jakákoliv dvě čísla x, y platí buď x ≤ y, nebo y ≤ x.

Plná relace: Relaci nazveme plnou, právě když . Plná relace tedy obsahuje celý kartézský součin. Pozor: úplná a plná relace jsou dva rozličné pojmy!

Prázdná relace: Relaci nazveme prázdnou, jestliže . Jedná se tedy o prázdnou množinu.

Nyní se podíváme na dvě speciální relace a to relaci ekvivalence a relaci uspořádání.

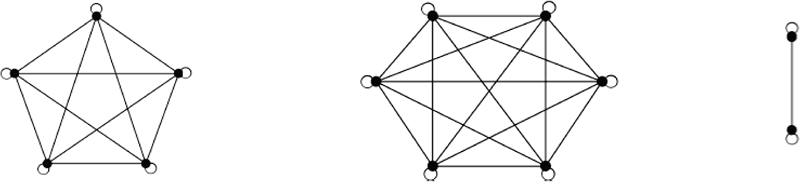
Relace ekvivalence: Relaci nazveme ekvivalence, právě když je tato relace reflexivní, symetrická a tranzitivní. Ekvivalence je určitým zobecněním rovnosti (tedy identity). Je zřejmé, že rovnost splňuje všechny tři požadované vlastnosti ekvivalence, tj. je reflexivní (každý prvek je roven sám sobě), symetrická (je-li jeden roven druhému, je i druhý roven prvnímu), i tranzitivní (pokud a = b a b = c, pak i a = c). Existují však i jiné vlastnosti, které splňují tyto tři podmínky. Jejich společným jmenovatelem je to, že v definici relace musí být popsána vlastnost, která je stejná pro prvky, které spolu jsou v relaci. Typickými příklady tak jsou "dávat po dělení číslem m stejný zbytek", "mít stejné znaménko", apod. V případě ekvivalence se lze někdy setkat s označením ~, či ≈. Na následujícím obrázku si pomocí grafu můžeme znázornit, jak taková relace ekvivalence vypadá (absence šipek je způsobena symetrií relace).

Příklad: Nechť M je množina všech studentů. Uvažujme postupně následující relace R ⊆ M × M a zjistěte, zda-li se jedná o ekvivalence

• (x,y) ∈ R právě když x má stejnou výšku jako y

• (x,y) ∈ R právě když x má stejnou barvu vlasů jako y

• (x,y) ∈ R právě když x a y mají stejnou výšku a barvu vlasů

• (x,y) ∈ R právě když x a y mají stejnou výšku nebo barvu vlasů

Řešení

Kromě posledního případu jsou všechny relace ekvivalence. U posledního případu není splněna tranzitivita.

Příklad: Nechť R ⊆ ℕ × ℕ je binární relace definována následujícím způsobem: (x, y) ∈ R právě tehdy, když |x-y| je dělitelné třemi. V jakém smyslu jsou x a y stejné?

Řešení

Dávají stejný zbytek po dělení třemi.

Rozklad množiny: Nechť  je množina. Rozklad na množině  je taková množina podmnožin , která splňuje následující podmínky:

Prvkům  se také říká třídy rozkladu. S relacemi ekvivalence a jimi implicitně definovanými rozklady množin se lze setkat tam, kde nějaké objekty "rozdělujeme do přihrádek" podle nějakých sdílených znaků nebo jiných kritérií.

Příklad:

Buď M = {a,b,c,d}. Pak N = {{a}, {b,c},{d}} je rozklad na M.

Nechť A₀ = {k ∉ ℕ | k mod 3 = 0}, A₁ = {k ∉ ℕ | k mod 3 = 1} a A₂ = {k ∉ ℕ | k mod 3 = 2}. Pak N = {A₀, A_1, A₂} je rozklad všech přirozených čísel podle zbytkových tříd.

Relace uspořádání: Relaci nazveme uspořádáním, právě když je reflexivní, antisymetrická a tranzitivní. Uspořádání zde máme, podobně jako tomu bylo v případě ekvivalence, definováno velmi obecně, tj. jde nám o to, abychom byli schopni vybudovat na prvcích dané množiny stromovou strukturu. Nechceme tedy uspořádat prvky množiny do jediného řetězce, jak by mohlo z významu slova "uspořádání" plynout, obecnost spočívá právě v tom, že jeden prvek může mít v daném uspořádání více následníků, vždy má však jen jediného předchůdce. Typickým uspořádáním je relace ≤, tedy "být menší nebo rovno".

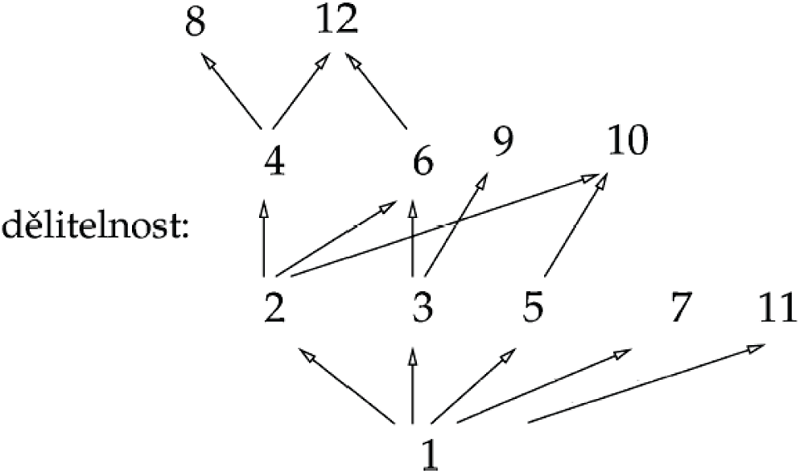
Na následujícím obrázku je graficky znázorněna relace uspořádání pomocí dělitelnosti. V obrázku jsou zakresleny jen šipky vyplývající z antisymetrie (šipky vyplývající z reflexivity a tranzitivity jsou vynechány).

Příklad: Dokažte, že relace ρ = {(a,b) ∈ ℤ² | (a ≤  b)} je uspořádání.

Řešení

Je třeba ověřit, že uvedená relace je reflexivní, antisymetrická a tranzitivní.

           Reflexivita: Je zřejmé, že pro každé celé číslo z platí, že z ≤ z. Relace je tedy reflexivní.

           Antisymetrie: Je třeba ověřit, že pro každou dvojici celých čísel platí, že je-li x ≤ y a zároveň y ≤ x, pak je nutně x = y. To je však také snadné. Je-li x ≤ y, pak je buď x < y, nebo x = y. Stejně tak, je-li y ≤ x, pak je buď y < x, nebo y = x. Zamyslíme-li se nad tím, které ze čtyř možných kombinací uvedených dvojic nevedou ke sporu, je evidentní, že dostáváme x = y. Relace je tedy antisymetrická.

           Tranzitivita: Je třeba ověřit, že je-li x ≤ y a y ≤ z, pak je i x ≤ z, což je však evidentní.

Uvedená relace je reflexivní, antisymetrická a tranzitivní, je to tedy uspořádání.